I en isobarisk process, trycket P av ett system förblir konstant. Prefixet "iso" kommer från grekiska och används för att beteckna att något förblir konstant, medan "baros", även från grekiska, betyder vikt.
Isobara processer är mycket typiska både i slutna behållare och i öppna utrymmen, eftersom de är lätta att lokalisera i naturen. Med detta menar vi att det är möjliga fysiska och kemiska förändringar på jordytan eller kemiska reaktioner i behållare som är öppna för atmosfären..
Några exempel erhålls genom att värma en ballong fylld med luft i solen, koka, koka eller frysa vatten, ånga som genereras i pannor eller genom att lyfta en varmluftsballong. Senare kommer vi att ge en förklaring av dessa fall.
Artikelindex
Låt oss härleda en ekvation för den isobara processen, förutsatt att systemet som studeras är en idealisk gas, en modell som är ganska lämplig för nästan vilken gas som helst vid mindre än 3 atmosfärer av tryck. De ideala gaspartiklarna rör sig slumpmässigt och upptar hela volymen i utrymmet som innehåller dem utan att interagera med varandra..
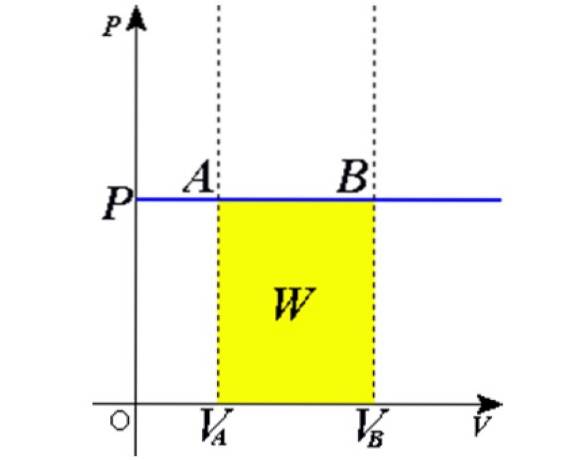
Om den ideala gasen som är innesluten i en cylinder utrustad med en rörlig kolv tillåts expandera långsamt, kan man anta att dess partiklar alltid är i jämvikt. Sedan utövar gasen på områdets kolv TILL en kraft F av storlek:
F = p.A
Var sid är gasens tryck. Denna kraft utövar arbete som producerar en oändlig förskjutning dx på kolven från:
dW = Fdx = pA.dx
Som produkten Adx är en volymdifferens dV, sedan dW = pdV. Det återstår att integrera båda sidor från den ursprungliga volymen VTILL tills slutvolymen VB för att få det totala arbetet som utförs av gasen:
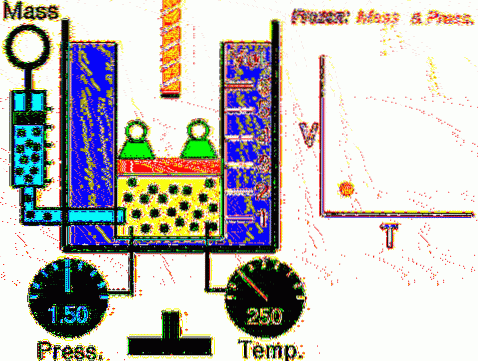
Den beskrivna situationen verifieras experimentellt genom att begränsa en gas inuti en cylinder försedd med en rörlig kolv, såsom visas i figurerna 2 och 3. En vikt av massa M placeras på kolven, vars vikt riktas nedåt medan gasen utövar en uppåtgående kraft tack vare trycket P som produceras på kolven.
Eftersom kolven kan röra sig fritt kan volymen som gasen upptar förändras utan problem, men trycket förblir konstant. Lägga till atmosfärstrycket Pbankomat, som också utövar en nedåtgående kraft har vi:
Mg - P.A + Pbankomat . A = konstant
Därför: P = (Mg / A) + Pbankomat den varierar inte, såvida inte M och därmed vikten modifieras. Genom att tillföra värme till cylindern expanderar gasen genom att öka volymen eller så kommer den att krympa när värme utvinns..
Den ideala gasekvationen för tillstånd relaterar till variablerna av betydelse: tryck P, volym V och temperatur T:
P.V = n. R.T.
Här representerar n antalet mol och R är den ideala gaskonstanten (giltig för alla gaser), som beräknas genom att multiplicera Boltzmanns konstant med Avogadros antal, vilket resulterar i:
R = 8,31 J / mol K
När trycket är konstant kan tillståndsekvationen skrivas som:
V / T = nR / P
Men nR / P är konstant, eftersom n, R och P är. Så när systemet går från tillstånd 1 till tillstånd 2 uppstår följande andel, även känd som Charles lag:
V1/ T1 = Vtvå/ Ttvå
Byt ut i W = PAV, det arbete som utförts för att gå från tillstånd 1 till tillstånd 2 erhålls, i termer av konstanter och temperaturvariationer, lätt att mäta med en termometer:
W1 → 2 = nR (T.två - T1) = nR.AT
Å andra sidan säger termodynamikens första lag att:
∆U = Q - W
Detta innebär att tillsättning av en viss mängd värme Q till gasen ökar den inre energin ∆U och ökar vibrationerna i dess molekyler. På detta sätt expanderar gasen och fungerar genom att flytta kolven, som vi har sagt tidigare..
I en monatomisk idealgas och variationen av den inre energin ∆U, som inkluderar både kinetisk energi och den potentiella energin hos dess molekyler, är:
∆U = (3/2)nR AT
Slutligen kombinerar vi de uttryck som vi har fått i ett:
F = ∆U + W = (3/2)nR AT + nR∆T = (5/2) nR AT
Alternativt kan Q skrivas om i termer av massan m, temperaturskillnaden och en ny konstant som kallas specifik gasvärme vid konstant tryck, förkortat csid, vars enheter är J / mol K:
Q = m csid ∆T
Inte alla isobara processer utförs i slutna behållare. Faktum är att otaliga termodynamiska processer av alla slag inträffar vid atmosfärstryck, så isobara processer är mycket frekventa i naturen. Detta inkluderar fysiska och kemiska förändringar på jordytan, kemiska reaktioner i kärl som är öppna för atmosfären och mycket mer..
För att isobariska processer ska kunna inträffa i slutna system måste deras gränser vara tillräckligt flexibla för att möjliggöra volymändringar utan varierande tryck.
Detta var vad som hände i kolvförsöket som rörde sig lätt när gasen expanderade. Samma sak händer med en gas i en festballong eller en luftballong.
Här har vi flera exempel på isobara processer:
Kokande vatten för te eller tillagning av såser i öppna behållare är bra exempel på isobariska processer, eftersom de alla äger rum vid atmosfärstryck..
När vattnet värms upp ökar temperaturen och volymen och om värmen fortsätter att tillsättas, når kokpunkten slutligen, i vilken fasförändringen av vattnet från vätska till vattenånga sker. Medan detta inträffar förblir temperaturen också konstant vid 100 ° C..
Å andra sidan är frysvatten också en isobarisk process, oavsett om den äger rum i en sjö under vintern eller i hemmakylskåpet..
Ett annat exempel på en isobar process är förändringen i volymen på en ballong som blåses upp med luft när den lämnas exponerad för solen. Först på morgonen, när det inte är särskilt varmt ännu, har ballongen en viss volym..
När tiden går och temperaturen ökar värms också ballongen upp och ökar dess volym och allt detta sker vid konstant tryck. Ballongens material är ett bra exempel på en kant som är tillräckligt flexibel så att luften inuti den vid uppvärmning expanderar utan att ändra trycket.
Upplevelsen kan också utföras genom att justera den icke uppblåsta ballongen i pipen på en glasflaska fylld med en tredjedel vatten, som värms upp i en bain-marie. Så snart vattnet värms upp blåser ballongen omedelbart, men man måste vara försiktig så att den inte värms för mycket så att den inte exploderar..
Det är ett flytande fartyg utan framdrivning, som använder luftströmmar för att transportera människor och föremål. Ballongen är vanligtvis fylld med varm luft, som kallare än den omgivande luften stiger och expanderar och får ballongen att stiga..
Även om luftströmmarna riktar ballongen, har den brännare som aktiveras för att värma upp gasen när det är önskvärt att stiga upp eller upprätthålla höjden, och avaktiveras vid nedstigning eller landning. Allt detta händer vid atmosfärstryck, antaget konstant i en viss höjd inte långt från ytan..
Ånga genereras i pannor genom att värma upp vatten och hålla trycket konstant. Därefter utför denna ånga ett användbart jobb, till exempel att generera elektricitet i termoelektriska anläggningar eller aktivera andra mekanismer som lok och vattenpumpar..
Det finns 40 liter gas vid en temperatur på 27 ºC. Hitta ökningen i volym när värme tillsätts isobariskt tills den når 100 ºC.
Charles lag används för att bestämma den slutliga volymen, men uppmärksamhet: temperaturerna måste uttryckas i kelvin, bara lägga till 273 K till var och en:
27 ºC = 27 + 273 K = 300 K
100 ºC = 100 + 273 K = 373 K
Från:
V1/ T1 = Vtvå/ Ttvå ⇒ Vtvå = Ttvå(V1/ T1) = 373 ºC (40 L / 300 K) = 49,7 L
Slutligen är volymökningen V.två - V1 = 49,7 L - 40 L = 9,7 L.
Levereras 5,00 x 103 J av energi till en idealisk gas för att utföra 2,00 x 103 J arbetar med sin miljö i en isobarisk process. Det ombeds att hitta:
a) Förändringen av gasens inre energi.
b) Volymförändringen, om nu den interna energin minskar med 4,50 x 103 J och 7,50 x 10 matas ut3 J i systemet, med tanke på konstant tryck på 1,01 x 105 Pa.
Begagnade ∆U = Q - W och värdena i uttalandet ersätts: Q = 5,00 x 103 J och W = 2,00 x 103 J:
=5,00 x 103 J - 2,00 x 103 J = 3,00 x 103 J
Därför ökar gasens inre energi med 3,00 x 103 J.
Volymförändringen återfinns i det utförda arbetet: W = P∆V:
∆U = Q - W = Q - P∆V
Uttalandet säger att den inre energin minskar, därför: ∆U= -4,50 x 103 J. Det berättar också för oss att en viss mängd värme matas ut: Q = -7,50 x 103 J. I båda fallen representerar det negativa tecknet minskning och förlust, så:
-4,50 x 103 J = -7,50 x 103 J - P∆V
Var P = 1,01 x 105 Pa. Eftersom alla enheter finns i det internationella systemet fortsätter vi med att lösa volymförändringen:
∆V = (-4,50 x 103 J +7,50 x 103 J) / (- 1,01 x 105 Pa) = -2,97 x 10-två m3
Eftersom volymförändringen är negativ betyder det att volymen minskade, det vill säga systemet kontraherade.
Ingen har kommenterat den här artikeln än.