
Låsegenskap för algebra-bevis, exempel
De lås egendom algebra är ett fenomen som relaterar två element i en uppsättning med en operation, där det nödvändiga villkoret är att, efter att de 2 elementen har behandlats under nämnda operation, tillhör resultatet också den ursprungliga uppsättningen.
Till exempel, om jämna tal tas som en uppsättning och en summa som en operation, får vi ett lås av den uppsättningen med avseende på summan. Detta beror på att summan av två jämna siffror alltid ger ytterligare ett jämnt antal och därmed uppfyller låsvillkoret.

Artikelindex
- 1 Funktioner
- 2 Antal algebra
- 3 Demo
- 3.1 Summa
- 3.2 Multiplikation
- 4 Särskilda fall i R
- 4.1 Uppdelning
- 4.2 Arkivering
- 4.3 Logaritm
- 5 Exempel
- 5.1 Summa i N
- 5.2 Subtraktion i N
- 6 Föreslagna övningar
- 7 Referenser
Egenskaper
Det finns många egenskaper som bestämmer algebraiska utrymmen eller kroppar, såsom strukturer eller ringar. Låsegenskapen är dock en av de mest kända inom grundalgebra.
Inte alla tillämpningar av dessa egenskaper är baserade på numeriska element eller fenomen. Många vardagliga exempel kan bearbetas utifrån ett rent algebraisk-teoretiskt synsätt.
Ett exempel kan vara medborgare i ett land som antar ett juridiskt förhållande av något slag, såsom ett kommersiellt partnerskap eller äktenskap bland andra. Efter att denna operation eller ledning har genomförts förblir de medborgare i landet. På detta sätt utgör medborgarskap och förvaltning med avseende på två medborgare ett lås.
Numerisk algebra
När det gäller siffror finns det många aspekter som har studerats i olika strömmar inom matematik och algebra. Ett stort antal axiomer och teormer har framkommit från dessa studier som tjänar som den teoretiska grunden för samtida forskning och arbete..
Om vi arbetar med de numeriska uppsättningarna kan vi skapa en annan giltig definition för låsegenskapen. En uppsättning A sägs vara låset för en annan uppsättning B om A är den minsta uppsättningen som innehåller alla uppsättningar och operationer som B rymmer..
Demonstration
Låssäkerheten tillämpas för element och operationer som finns i uppsättningen reella tal R.
Låt A och B vara två tal som tillhör uppsättningen R, stängningen av dessa element definieras för varje operation som ingår i R.
Belopp
- Summa: ∀ A ˄ B ∈ R → A + B = C ∈ R
Detta är det algebraiska sättet att säga det För alla A och B som tillhör de verkliga siffrorna har vi att summan av A plus B är lika med C, vilket också tillhör de verkliga siffrorna.
Det är lätt att kontrollera om detta förslag är sant; det räcker att genomföra summan mellan vilket verkligt tal som helst och kontrollera om resultatet också hör till de verkliga siffrorna.
3 + 2 = 5 ∈ R
-2 + (-7) = -9 R
-3 + 1/3 = -8/3 ∈ R
5/2 + (-2/3) = 11/6 ∈ R
Det observeras att låsvillkoret är uppfyllt för de verkliga siffrorna och summan. På detta sätt kan man dra slutsatsen: Summan av verkliga tal är ett algebraiskt lås.
Multiplikation
- Multiplikation: ∀ A ˄ B ∈ R → A. B = C ∈ R
För alla A och B som tillhör realerna har vi att multiplikationen av A med B är lika med C, vilket också tillhör realerna.
När du verifierar med samma element i föregående exempel observeras följande resultat.
3 x 2 = 6 ∈ R
-2 x (-7) = 14 ° R
-3 x 1/3 = -1 ∈ R
5/2 x (-2/3) = -5/3 ∈ R
Detta är tillräckligt med bevis för att dra slutsatsen att: Multiplikation av reella tal är ett algebraiskt lås.
Denna definition kan utvidgas till att omfatta alla operationer på verkliga tal, även om vi hittar vissa undantag.

Särskilda fall i R
Division
Som det första specialfallet observeras delningen, där följande undantag observeras:
∀ A ˄ B ∈ R → A / B ∉ R ↔ B = 0
För alla A och B som tillhör R vi har att A bland B inte tillhör realerna om och bara om B är lika med noll.
Detta fall hänvisar till begränsningen att inte kunna dela med noll. Eftersom noll tillhör de verkliga siffrorna dras slutsatsen att: lUppdelningen är inte ett lås på reals.
Arkivering
Det finns också potentieringsoperationer, mer specifikt de för radikalisering, där undantag presenteras för radikala krafter med jämnt index:
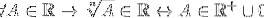
För alla A som tillhör realerna tillhör den nte roten till A till realerna, om och bara om A tillhör de positiva realerna förenade med en uppsättning vars enda element är noll.
På detta sätt betecknas det att de jämna rötterna endast gäller för positiva realer och det dras slutsatsen att potentiering inte är ett lås i R.
Logaritm
På ett homologt sätt kan det ses för den logaritmiska funktionen, som inte definieras för värden mindre än eller lika med noll. För att kontrollera om logaritmen är ett lås av R, gör så här:
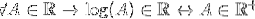
För alla A som tillhör realerna hör logaritmen till A till realerna, om och bara om A tillhör de positiva realerna.
Genom att utesluta negativa värden och noll som också tillhör R kan man säga att:
Logaritmen är inte ett lås för de verkliga siffrorna.
Exempel
Kontrollera låset för att addera och subtrahera naturliga tal:
Summa i N
Det första är att kontrollera låsförhållandet för olika element i den givna uppsättningen, där om det observeras att något element bryter mot villkoret kan förekomsten av ett lås automatiskt nekas.
Den här egenskapen gäller för alla möjliga värden på A och B, som observeras i följande operationer:
1 + 3 = 4 ∈ N
5 + 7 = 12 ∈ N
1000 + 10000 = 11000 ∈ N
Det finns inga naturvärden som bryter låsförhållandet, så det dras slutsatsen:
Summan är ett lås i N.
Subtrahera i N
De letar efter naturliga element som kan bryta tillståndet; A - B tillhör de infödda.
Manövrering är lätt att hitta par av naturliga element som inte uppfyller låsförhållandet. Till exempel:
7 - 10 = -3 ∉ a N
På detta sätt kan vi dra slutsatsen att:
Subtraktion är inte ett lås av uppsättningen naturliga tal.
Föreslagna övningar
1-Visa om låsegenskapen är uppfylld för uppsättningen rationella nummer Q, för operationernas addition, subtraktion, multiplikation och division.
2-Förklara om uppsättningen av reella tal är ett lås av uppsättningen heltal.
3-Bestäm vilken numerisk uppsättning som kan låsas för de verkliga siffrorna.
4-Bevisa låsegenskapen för uppsättningen imaginära tal, med avseende på addition, subtraktion, multiplikation och delning.
Referenser
- Panorama över ren matematik: valet från Bourbakist. Jean Dieudonné. Reverte, 1987.
- Algebraisk talteori. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. National Autonomous University of Mexico, 1975.
- Linjär algebra och dess tillämpningar. Sandra Ibeth Ochoa García, Eduardo Gutiérrez González.
- Algebraiska strukturer V: kroppsteori. Hector A. Merklen. Organisationen av amerikanska stater, generalsekretariatet, 1979.
- Introduktion till kommutativ algebra. Michael Francis Atiyah, I. G. MacDonald. Reverte, 1973.


Ingen har kommenterat den här artikeln än.