
Förklaring av sammansatt proportionalitet, sammansatt regel av tre, övningar
De förening eller multipel proportionalitet Det är förhållandet mellan mer än två magnituder, där direkt och omvänd proportionalitet kan observeras mellan data och det okända. Detta är en mer avancerad version av enkel proportionalitet, även om teknikerna som används i båda förfarandena är likartade..
Till exempel, om 7 personer behövs för att lossa 10 ton varor på 3 timmar, kan sammansatt proportionalitet användas för att beräkna hur många människor det tar att lossa 15 ton på 4 timmar..
För att svara på den här frågan är det bekvämt att göra en tabell över värden för att studera och relatera storheter och okända.
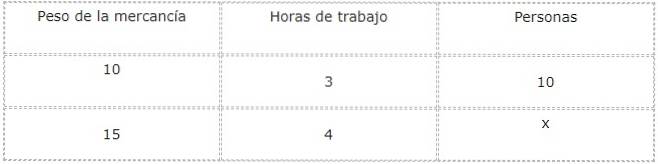
Vi fortsätter med att analysera typerna av förhållanden mellan varje storlek och den nuvarande okända, vilket i detta fall motsvarar antalet personer som kommer att arbeta.
När varans vikt ökar ökar antalet personer som krävs för att lossa den. På grund av detta är förhållandet mellan vikt och arbetare direkt.
Å andra sidan, när antalet arbetstagare ökar minskar arbetstiden. På grund av detta är förhållandet mellan människor och arbetstid av den omvända typen.
Artikelindex
- 1 Hur man beräknar sammansatta proportioner
- 2 Förklaring
- 3 Direkt regel om tre
- 4 Omvänd regel om tre
- 5 skick
- 6 Verifiering av resultat
- 7 Rensning
- 8 Historia
- 9 Lösta övningar
- 9.1 Övning 1
- 9.2 Övning 2
- 10 Föreslagna övningar
- 11 Referenser
Hur man beräknar sammansatta proportioner
För att lösa exempel som ovan används mestadels sammansättningsregeln för tre. Detta består i att fastställa typerna av förhållanden mellan storheter och okända och sedan representera en produkt mellan fraktioner.
Med avseende på det ursprungliga exemplet är de fraktioner som motsvarar värdetabellen organiserade enligt följande:
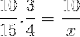
Men innan man löser och löser det okända måste fraktionerna som motsvarar det omvända förhållandet inverteras. Vilket i detta fall motsvarar den variabla tiden. På detta sätt kommer den åtgärd som ska lösas att vara:
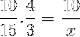
Vars enda skillnad är inversionen av fraktionen som motsvarar tidsvariabeln 4/3. Vi fortsätter att arbeta och rensa värdet på x.
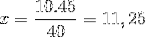
Således behövs mer än elva personer för att kunna lossa 15 ton varor på fyra timmar eller mindre.
Förklaring
Proportionalitet är det ständiga förhållandet mellan storheter som kan förändras, vilket kommer att vara symmetriskt för var och en av de berörda storheterna. Det finns direkta och omvänt proportionella förhållanden, vilket definierar parametrarna för enkel eller sammansatt proportionalitet.
Direkt regel om tre
Den består av ett proportionellt förhållande mellan variabler som visar samma beteende när de ändras. Det är mycket frekvent vid beräkningen av procenttal som hänvisar till andra storleksstorlekar än hundra, där dess grundläggande struktur uppskattas.
Som ett exempel kan 15% av 63 beräknas. Vid första anblicken kan denna procentsats inte lätt uppskattas. Men genom att implementera regeln om tre kan följande förhållande göras: om 100% är 63, då 15%, hur mycket blir det?
100% - 63
15% -X
Och motsvarande operation är:
(15%. 63) / 100% = 9,45
Där procentsatserna förenklas och siffran 9.45 erhålls, vilket motsvarar 15% av 63.
Omvänd regel om tre
Som namnet antyder är förhållandet mellan variablerna i det här fallet motsatt. Det omvända förhållandet måste fastställas innan du fortsätter till beräkningen. Dess förfarande är homologt med det för den direkta regeln om tre, förutom att investeringen i den bråk som ska beräknas..
Till exempel behöver 3 målare 5 timmar för att avsluta en vägg. På hur många timmar skulle fyra målare avsluta det?
I det här fallet är förhållandet inverterat, eftersom antalet målare ökar bör arbetstiden minska. Förhållandet är etablerat;
3 målare - 5 timmar
4 målare - X timmar
När förhållandet är omvänd, omvändes arbetsordningen. Detta är rätt sätt;
(3 målare). (5 timmar) / 4 målare = 3,75 timmar
Termen målare förenklas och resultatet är 3,75 timmar.
Tillstånd
För att vara i närvaro av en förening eller multipel proportionalitet är det nödvändigt att hitta båda typerna av samband mellan storheterna och variablerna.
- Direkt: Variabeln har samma beteende som det okända. Det vill säga, när en ökar eller minskar, ändras den andra lika.
- Invers: variabeln presenterar ett antonymbeteende för det okända. Den bråk som definierar nämnda variabel i värdetabellen måste inverteras för att representera det omvänt proportionella förhållandet mellan variabel och okänd..
Verifiering av resultat
Det är mycket vanligt att förvirra storleksordningen när man arbetar med sammansatta proportioner, till skillnad från vad som händer i de vanliga proportionberäkningarna, vars natur mestadels är direkt och lösbar med en enkel regel på tre..
Av denna anledning är det viktigt att undersöka den logiska ordningen på resultaten och verifiera sammanhållningen av de siffror som produceras av regeln om tre sammansatta.
I det första exemplet skulle det vara 20 att göra ett sådant misstag. Det vill säga 20 personer för att lossa 15 ton varor på fyra timmar.
Vid första anblicken verkar det inte som ett galet resultat, men det är märkligt en personalökning på nästan 200% (från 7 till 20 personer) när ökningen av varor är 50%, och till och med med en större tidsrymd att utföra arbetet.
På detta sätt utgör den logiska verifieringen av resultaten ett viktigt steg när man implementerar regeln om tre föreningar..
Undanröjning
Även om mer grundläggande till sin natur med avseende på matematisk träning, är clearingen ett viktigt steg i fall av proportionalitet. Ett felaktigt godkännande räcker för att ogiltigförklara alla resultat som erhållits i den enkla eller sammansatta regeln om tre..
Berättelse
Regeln om tre blev känd i väst genom araberna, med publikationer av olika författare. Bland dem Al-Jwarizmi och Al-Biruni.
Tack vare sin mångkulturella kunskap hade Al-Biruni tillgång till omfattande information om denna praxis under sina resor till Indien, ansvarig för den mest omfattande dokumentationen om regeln om tre.
Han hävdar i sin forskning att Indien var den första platsen där användningen av regeln om tre blev vanlig. Författaren försäkrar att den utfördes på ett flytande sätt i dess direkta, inversa och till och med komponerade versioner..
Det exakta datumet då regeln om tre blev en del av den matematiska kunskapen i Indien är fortfarande okänd. Emellertid upptäcktes det äldsta dokumentet som behandlar denna praxis, Bakhshali-manuskriptet 1881. Det finns för närvarande i Oxford.
Många matematikhistoriker hävdar att detta manuskript är från början av den nuvarande eran..
Lösta övningar
Övning 1
Ett flygbolag måste ha 1 535 personer. Det är känt att det med tre plan skulle ta 12 dagar att få den sista passageraren till destinationen. 450 fler personer har anlänt till flygbolaget och två flygplan beställs att repareras för att hjälpa till med denna uppgift. Hur många dagar tar det flygbolaget att överföra den sista passageraren till sin destination?
Förhållandet mellan antalet personer och arbetsdagar är direkt, för ju större antal människor desto fler dagar tar det att utföra detta arbete..
Å andra sidan är förhållandet mellan flygplan och dagar omvänt proportionellt. När antalet flygplan ökar minskar antalet dagar som behövs för att överföra alla passagerare.
Tabellen över värden som hänvisar till detta fall görs.

Som detaljerat i det ursprungliga exemplet måste täljaren och nämnaren vara inverterad i den bråk som motsvarar den inversa variabeln med avseende på det okända. Funktionen är som följer:
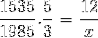
X = 71460/7675 = 9,31 dagar
För att överföra 1985-personer med 5 plan tar det mer än 9 dagar.
Övning 2
En 25-ton majsskörd tas till lastbilarna. Det är känt att det föregående år tog dem 8 timmar med en löner på 150 arbetare. Om lönelistan för detta år ökade med 35%, hur lång tid tar det att fylla lastbilarna med en 40-ton skörd??
Innan värdetabellen representeras måste antalet arbetare för detta år definieras. Detta ökade med 35% från den ursprungliga siffran om 150 arbetare. För detta används en direktregel på tre.
100% - 150
35% - X
X = (35,100) / 100 = 52,5. Detta är antalet ytterligare arbetstagare i förhållande till föregående år, som får totalt 203 arbetare efter avrundning av det erhållna beloppet.
Vi fortsätter med att definiera motsvarande datatabell

I detta fall representerar vikten en variabel som är direkt relaterad till den okända tiden. Å andra sidan har arbetstagarvariabeln en omvänd relation med tiden. Ju större antal arbetare, desto kortare arbetsdag.
Med hänsyn till dessa överväganden och invertera den bråk som motsvarar arbetstagarvariabeln fortsätter vi med att beräkna.
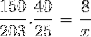
X = 40600/6000 = 6,76 timmar
Dagen tar knappt sju timmar.
Föreslagna övningar
- Definiera 73% av 2875.
- Beräkna antalet timmar som Teresa sover, om det är känt att hon bara sover 7% av totalen för dagen. Definiera hur många timmar du sover i veckan.
- En tidning publicerar 2000 exemplar var 5: e timme och använder endast två tryckmaskiner. Hur många exemplar kommer han att producera på en timme, om han använder 7 maskiner? Hur lång tid tar det 10 000 exemplar med 4 maskiner?
Referenser
- Encyclopedia Alvarez-initiering. A. Álvarez, Antonio Álvarez Pérez. EDAF, 2001.
- Komplett grundläggande och högre grundinstruktionsmanual: för användning av blivande lärare och särskilt elever från provinsens normala skolor, volym 1. Joaquín Avendaño. Utskrift av D. Dionisio Hidalgo, 1844.
- Rationell tillnärmning av verkliga funktioner. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 mars. 2011.
- Grundläggande aritmetik för undervisning i skolor och högskolor i Centralamerika. Darío González. Dricks. Arenales, 1926.
- Studiet av matematik: Om matematikens studier och svårigheter. Augustus De Morgan. Baldwin och Cradock, 1830.

Ingen har kommenterat den här artikeln än.