De rang, avstånd eller amplitud, i statistik, är skillnaden (subtraktion) mellan maximivärdet och minimivärdet för en uppsättning data från ett urval eller en population. Om intervallet representeras av bokstaven R och data med x, formeln för intervallet är helt enkelt:
R = xmax - xmin
Där xmax är det maximala värdet på data och xmin är det minsta.
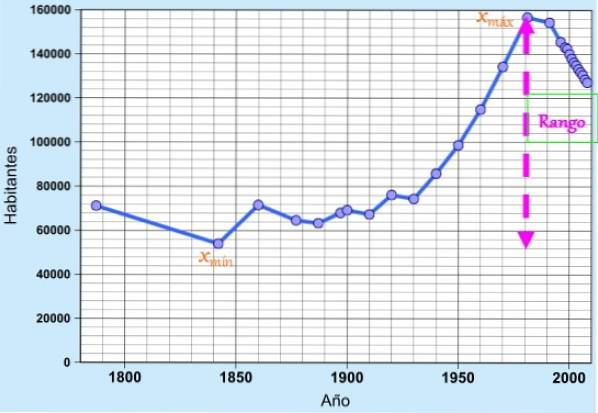
Konceptet är mycket användbart som ett enkelt mått på spridning för att snabbt uppskatta datavariabiliteten, eftersom det indikerar förlängningen eller längden på intervallet där dessa finns..
Antag till exempel att höjden på en grupp av 25 manliga förstaårs ingenjörsstudenter vid ett universitet mäts. Den högsta studenten i gruppen är 1,93 m och den kortaste 1,67 m. Dessa är de extrema värdena för samplingsdata, därför är deras väg:
R = 1,93 - 1,67 m = 0,26 m eller 26 cm.
Studenternas höjd i denna grupp fördelas längs detta intervall.
Artikelindex
Räckvidd är, som vi sa tidigare, ett mått på hur utspridda uppgifterna är. Ett litet intervall indikerar att data är mer eller mindre nära och att det är lite spridning. Å andra sidan indikerar ett större intervall att data är mer spridda..
Fördelarna med att beräkna intervallet är uppenbara: det är väldigt enkelt och snabbt att hitta, eftersom det är en enkel skillnad.
Den har också samma enheter som de data som den fungerar med och konceptet är väldigt lätt att tolka för alla observatörer..
I exemplet med ingenjörsstudenternas höjd, om intervallet hade varit 5 cm, skulle vi säga att eleverna alla är ungefär lika stora. Men med ett intervall på 26 cm antar vi omedelbart att det finns studenter av alla mellanhöjder i provet. Är detta antagande alltid korrekt?
Om vi tittar noga kan det hända att i vårt urval av 25 ingenjörsstudenter bara en av dem mäter 1,93 och de återstående 24 har höjder nära 1,67 m.
Och ändå förblir räckvidden densamma, även om det motsatta är helt möjligt: att majoritetens höjd är cirka 1,90 m och endast en är 1,67 m.
I båda fallen är distributionen av data helt annorlunda.
Nackdelarna med räckvidd som mått på spridning beror på att det bara använder extrema värden och ignorerar alla andra. Eftersom det mesta av informationen går förlorad har du ingen aning om hur exemplets data distribueras.
En annan viktig egenskap är att provets intervall aldrig minskar. Om vi lägger till mer information, det vill säga vi överväger mer data, ökar intervallet eller förblir detsamma.
Och i vilket fall som helst är det bara användbart när man arbetar med små prover, dess enda användning som mått på spridning i stora prover rekommenderas inte..
Vad du behöver göra är att komplettera med beräkningen av andra spridningsåtgärder som tar hänsyn till informationen från den totala informationen: rutt interkvartil, varians, standardavvikelse och variationskoefficient.
Vi har insett att svagheten i intervallet som ett mått på spridning är att det bara använder de extrema värdena för datadistributionen och utelämnar de andra..
För att undvika detta besvär bör kvartiler: tre värden kända som positionsmätningar.
De fördelar de icke-grupperade uppgifterna i fyra delar (andra allmänt använda positionsmått är deciler och den percentiler). Dessa är dess egenskaper:
-Den första kvartilen Q1 är värdet på data så att 25% av dem alla är mindre än Q1.
-Den andra kvartilen Qtvå är median av distributionen, vilket innebär att hälften (50%) av uppgifterna är mindre än det värdet.
-Slutligen den tredje kvartilen Q3 påpekar att 75% av uppgifterna är mindre än Q3.
Därefter definieras interkvartilintervallet eller interkvartilintervallet som skillnaden mellan den tredje kvartilen Q3 och den första kvartilen Q1 av uppgifterna:
Interkvartilintervall = RF = Q3 - F1
På detta sätt kan värdet för intervallet RF det påverkas inte lika mycket av extrema värden. Av denna anledning är det tillrådligt att använda den när man hanterar snedställda fördelningar, som de som beskrivs ovan för mycket långa eller mycket korta studenter..
Det finns flera sätt att beräkna dem, här kommer vi att föreslå ett, men i alla fall är det nödvändigt att känna till antal order "Neller”, Vilket är den plats som respektive kvartil upptar i distributionen.
Det vill säga om till exempel termen som motsvarar Q1 är den andra, tredje eller fjärde och så vidare av distributionen.
Neller (F1) = (N + 1) / 4
Neller (Qtvå) = (N + 1) / 2
Neller (Q3) = 3 (N + 1) / 4
Där N är antalet data.
Medianen är det värde som ligger mitt i distributionen. Om antalet data är udda finns det inga problem att hitta den, men om den är jämn, beräknas de två centrala värdena i genomsnitt för att bli ett.
När ordernumret har beräknats följs en av dessa tre regler:
-Om den inte har decimaler söks de data som anges i distributionen och detta kommer att vara den sökta kvartilen.
-När ordernumret är halvvägs mellan två beräknas de data som indikeras av heltalets medelvärde med följande data, och resultatet är motsvarande kvartil.
-I något annat fall avrundas det till närmaste heltal och det kommer att vara kvartilens position.
På en skala från 0 till 20 fick en grupp på 16 matematik I-studenter följande poäng (poäng) vid en mellantentamen:
16, 10, 12, 8, 9, 15, 18, 20, 9, 11, 1, 13, 17, 9, 10, 14
Hitta:
a) Datas omfång eller intervall.
b) Värdena för kvartilerna Q1 och Q3
c) Interkvartilintervallet.
Det första du ska göra för att hitta sökvägen är att beställa data i ökande eller minskande ordning. Till exempel i ökande ordning har du:
1, 8, 9, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20
Med formeln i början: R = xmax - xmin
R = 20 - 1 poäng = 19 poäng.
Enligt resultatet har dessa kvalifikationer en stor spridning.
N = 16
Neller (F1) = (N + 1) / 4 = (16 + 1) / 4 = 17/4 = 4,25
Det är ett tal med decimaler, vars heltal är 4. Sedan går vi till fördelningen, vi letar efter data som upptar fjärde platsen och dess värde beräknas i genomsnitt med den femte positionen. Eftersom de båda är 9 är genomsnittet också 9 och så:
F1 = 9
Nu upprepar vi proceduren för att hitta Q3:
Neller (F3) = 3 (N + 1) / 4 = 3 (16 +1) / 4 = 12,75
Återigen är det ett decimal, men eftersom det inte är halvvägs avrundas det till 13. Kvartilen vi letar efter intar den trettonde positionen och är:
F3 = 16
RF = Q3 - F1 = 16 - 9 = 7 poäng.
Som, som vi ser, är mycket mindre än det dataområde som beräknas i avsnitt a), eftersom minimipoängen var 1 poäng, ett värde mycket längre bort från resten..
Ingen har kommenterat den här artikeln än.