De dal i fysik Det är en benämning som används i studien av vågfenomen för att ange en vågs lägsta eller lägsta värde. Således betraktas en dal som en konkavitet eller depression.
När det gäller den cirkulära vågen som bildas på vattenytan när en droppe eller en sten faller, är fördjupningarna vågens dalar och utbuktningarna är åsarna.
Ett annat exempel är den våg som genereras i en stram sträng, vars ena ände gör att den svänger vertikalt medan den andra hålls fast. I det här fallet sprider sig den producerade vågen med en viss hastighet, har en sinusform och består också av dalar och åsar..
Ovanstående exempel hänvisar till tvärgående vågor, eftersom dalarna och åsarna löper tvärs eller vinkelrätt mot utbredningsriktningen..
Samma koncept kan emellertid tillämpas på längsgående vågor som ljud i luft, vars svängningar sker i samma riktning för förökning. Här kommer vågdalarna att vara de platser där luftens densitet är minimal och åsarna där luften är tätare eller komprimerad.
Artikelindex
Avståndet mellan två dalar, eller avståndet mellan två åsar, kallas våglängd och betecknas med det grekiska brevet λ. Samma punkt av en våg förändras från att vara i en dal till att vara en topp som svängningen sprids.
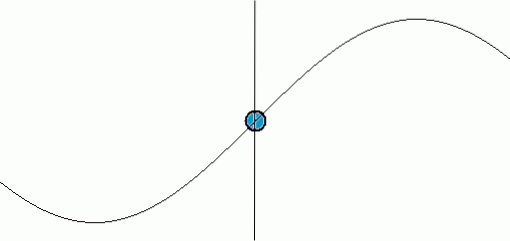
Tiden som går från en dal-krön-dal, i en fast position, kallas svingperiod och den här gången betecknas med ett stort t: T.
Under en period T vågen går fram en våglängd λ, det sägs därför hastighet v med vilken vågen går framåt är:
v = λ / T
Avståndet eller det vertikala avståndet mellan dalen och vågens topp är dubbelt så mycket som svängningens amplitud, det vill säga avståndet från en dal till centrum för den vertikala svängningen är amplitud A. Vinka.
En våg är harmonisk om dess form beskrivs av de matematiska funktionerna sinus eller cosinus. I allmänhet skrivs en harmonisk våg som:
y (x, t) = A cos (k⋅x ± ω⋅t)
I denna ekvation är variabeln Y representerar avvikelsen eller förskjutningen från jämviktspositionen (y = 0) vid position x Just nu t.
Parameter TILL är svängningens amplitud, en alltid positiv kvantitet som representerar avvikelsen från vågens dal till svängningens centrum (y = 0). I en harmonisk våg är det nöjd med att avvikelsen Y, från dalen till åsen är det A / 2.
Andra parametrar som visas i den harmoniska vågformeln, särskilt i sinusfunktionens argument, är vågnumret k och vinkelfrekvensen ω.
Vågnummer k är relaterad till våglängden λ med följande uttryck:
k = 2π / λ
Vinkelfrekvens ω är relaterad till perioden T genom:
ω = 2π / T
Observera att ± visas i sinusfunktionens argument, det vill säga i vissa fall tillämpas positivt tecken och i andra negativt tecken.
Om en våg som fortplantas i den positiva riktningen av x, då är det minustecknet (-) som ska appliceras. Annars, det vill säga i en våg som sprider sig i negativ riktning, appliceras det positiva tecknet (+)..
Utbredningshastigheten för en harmonisk våg kan skrivas som en funktion av vinkelfrekvensen och vågnumret enligt följande:
v = ω / k
Det är lätt att visa att detta uttryck är helt ekvivalent med det vi gav tidigare som en funktion av våglängd och period.
Ett barn leker vågor med ett klädstreckrep, för vilket han lossar ena änden och får det att svänga med en vertikal rörelse med en hastighet av 1 svängning per sekund.
Under denna process förblir barnet stilla på samma plats och rör bara armen uppåt och nedåt och tvärtom..
Medan pojken genererar vågorna tar hans äldre bror en bild av honom med sin mobil. När du jämför storleken på vågorna med bilen som står strax bakom repet, märker du att den vertikala åtskillnaden mellan dalar och åsar är densamma som höjden på bilrutorna (44 cm).
På bilden kan det också ses att separationen mellan två på varandra följande dalar är densamma som mellan bakkanten på bakdörren och framkanten på ytterdörren (2,6 m).
Med dessa data föreslår den äldre bror att hitta den harmoniska vågfunktionen antar som det första ögonblicket (t = 0) det ögonblick där hans lillebrors hand var på den högsta punkten..
Det antar också att x-axeln börjar (x = 0) vid handplatsen, med en positiv riktning framåt och passerar genom mitten av den vertikala svängningen. Med denna information kan du beräkna parametrarna för den harmoniska vågen:
Amplituden är halva höjden av en dal till en ås, det vill säga:
A = 44 cm / 2 = 22 cm = 0,22 m
Vågnumret är
k = 2π / (2,6 m) = 2,42 rad / m
När barnet höjer och sänker handen under en sekund kommer vinkelfrekvensen att vara
ω = 2π / (1 s) = 6,28 rad / s
Kort sagt är formeln för den harmoniska vågen
y (x, t) = 0,22m cos (2,42x - 6.28⋅t)
Vågens fortplantningshastighet kommer att vara
v = 6,28 rad / s/ 2,42 rad / m = 15,2 m / s
Den första dalen inom en sekund efter att handrörelsen startar kommer att vara på avståndet d av barnet och ges av följande relation:
y (d, 1s) = -0,22m = 0,22m cos (2,42dd - 6.28⋅1)
Vilket betyder att
cos (2,42d - 6,28) = -1
Nämligen
2,42d - 6,28 = -π
2.42⋅d = π
d = 1,3 m (position för dalen närmast t = 1s)
Vågor och mekaniska enkla harmoniska vågor. Återställd från: physicskey.com.
Ingen har kommenterat den här artikeln än.