Högerhand regel första och andra regel, applikationer, övningar

De högerhandregel är en minnesresurs för att fastställa riktningen och känslan för vektorn som härrör från en vektorprodukt eller tvärprodukt. Det används ofta i fysik, eftersom det finns viktiga vektormängder som är resultatet av en vektorprodukt. Så är exempelvis vridmoment, magnetisk kraft, vinkelmoment och magnetiskt moment.

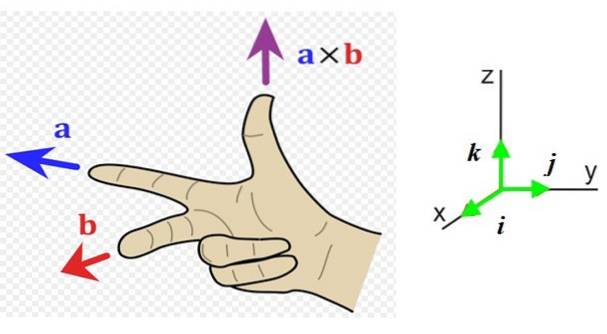
Låt vara två generiska vektorer till Y b vars tvärprodukt är till x b. Modulen för en sådan vektor är:

till x b = a.b. i α

Där α är minsta vinkel mellan till Y b, medan a och b representerar dess moduler. För att urskilja vektorerna i deras moduler används fetstil.

Nu måste vi veta riktningen och känslan för denna vektor, så det är bekvämt att ha ett referenssystem med de tre rymdriktningarna (figur 1 till höger). Enhetsvektorerna i, j Y k de pekar respektive mot läsaren (utanför sidan), till höger och uppåt.

I exemplet i figur 1 till vänster, vektorn till går till vänster (riktning Y negativa och pekfingret på höger hand) och vektorn b går till läsaren (riktning x positivt, långfinger på höger hand).

Den resulterande vektorn till x b har tumriktningen uppåt i riktningen z positiv.

Artikelindex

• 1 Andra regeln för höger hand
  • 1.1 Alternativ regel för höger hand
• 2 applikationer
  • 2.1 Vinkelhastighet och acceleration
  • 2.2 Vinkelmomentet
• 3 Övningar
  • 3.1 - Övning 1
  • 3.2 - Övning 2
• 4 Referenser

Andra regeln för höger hand

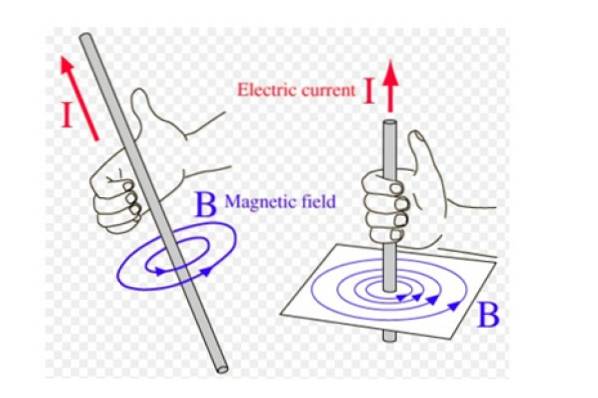
Denna regel, även kallad höger tumregel, Det används mycket när det finns magnituder vars riktning och riktning roterar, såsom magnetfältet B produceras av en tunn, rak tråd som bär en ström.

I detta fall är magnetfältlinjerna koncentriska cirklar med tråden, och rotationsriktningen erhålls med denna regel på följande sätt: höger tumme pekar i strömriktningen och de återstående fyra fingrarna är krökta i riktning mot landsbygden. Vi illustrerar konceptet i figur 2.

Alternativ högerhandregel

Figuren nedan visar en alternativ form av högerregeln. Vektorerna som visas i illustrationen är:

-Hastighet v av en punktladdning q.

-Magnetiskt fält B inom vilken lasten rör sig.

-F_B den kraft som magnetfältet utövar på laddningen.

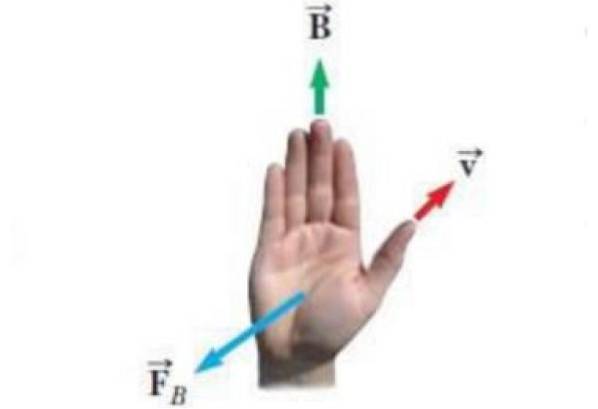
Ekvationen för den magnetiska kraften är F_B = qv x B och regeln för höger hand att känna riktningen och känslan av F_B appliceras så här: tummen pekar enligt v, de fyra återstående fingrarna placeras enligt fält B. Sedan F_B är en vektor som kommer ut ur handflatan, vinkelrät mot den, som om den trycker på lasten.

Anteckna det F_B Jag skulle peka i motsatt riktning om laddningen q var negativ, eftersom vektorprodukten inte är kommutativ. Faktiskt:

till x b = - b x till

Applikationer

Högerhandregeln kan tillämpas för olika fysiska kvantiteter, låt oss veta några av dem:

Vinkelhastighet och acceleration

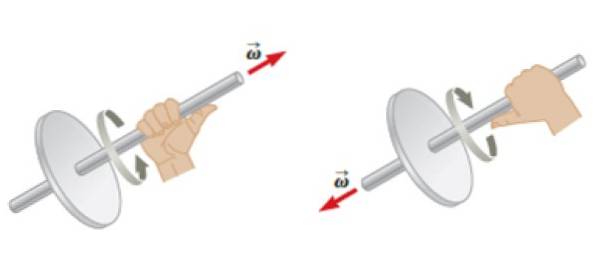
Båda vinkelhastigheterna ω som vinkelacceleration a de är vektorer. Om ett objekt roterar kring en fast axel är det möjligt att tilldela riktningen och avkänningen av dessa vektorer med hjälp av högerhandregeln: de fyra fingrarna är böjda efter rotation och tummen ger omedelbart riktningen och känslan av vinkelhastighet ω.

För sin del vinkelacceleration a kommer att ha samma adress som ω, men dess betydelse beror på om ω ökar eller minskar i storlek över tiden. I det första fallet har båda samma riktning och känsla, men i det andra kommer de att ha motsatta riktningar..

Vinkelmoment

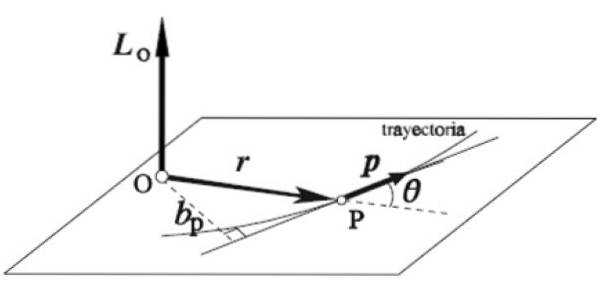
Vinkelmomentvektorn L_ELLER av en partikel som roterar runt en viss axel O definieras som vektorprodukten för dess momentana positionsvektor r  och linjär fart sid:

L = r x sid

Regeln för höger hand tillämpas på detta sätt: pekfingret placeras i samma riktning och känsla av r, långfingret på det av sid, båda på ett horisontellt plan, som i figuren. Tummen förlängs automatiskt vertikalt uppåt vilket indikerar riktningen och känslan av vinkelmoment L_ELLER.

Träning

- Övning 1

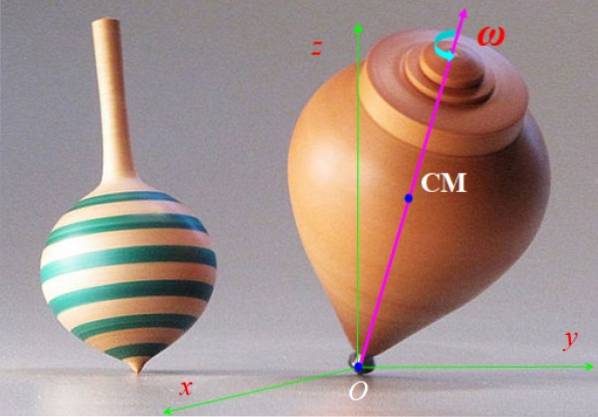
Toppen i figur 6 snurrar snabbt med vinkelhastighet ω och dess symmetriaxel roterar långsammare runt den vertikala axeln z. Denna rörelse kallas precession. Beskriv krafterna som verkar på snurret och effekten de ger.

Lösning

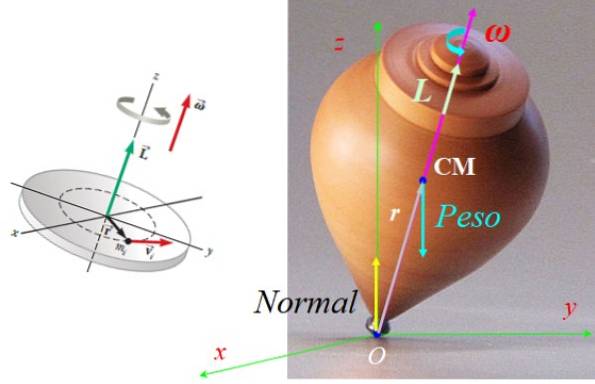
Krafterna som verkar på toppen är normala N, appliceras på stödpunkten med marken O plus vikten Mg, appliceras i centrum av massan CM, med g gravitationens accelerationsvektor, riktad vertikalt nedåt (se figur 7).

Båda krafterna balanserar, därför rör sig inte toppen. Men vikten ger ett vridmoment eller vridmoment τ netto med avseende på punkt O, ges av:

τ_ELLER = r_ELLER x F, med F = Mg.

Vad r och Mg de är alltid i samma plan som toppen roterar, enligt vridmomentet till höger τ_ELLER ligger alltid på planet xy, vinkelrätt mot båda r Vad g.

Anteckna det N producerar inte ett vridmoment med avseende på O, eftersom dess vektor r med avseende på O är noll. Detta vridmoment ger en förändring i vinkelmomentet som får toppen att gå före Z-axeln..

- Övning 2

Ange riktningen och känslan för vinkelmomentvektorn L på toppen av figur 6.

Lösning

Varje punkt på toppen har massa m_i, hastighet v_i och positionsvektor r_i, när den roterar runt z-axeln. Vinkelmoment L_i av nämnda partikel är:

L_i = r_i x sid_i = r_i x m_iv_i

Med tanke på r_i Y v_i är vinkelräta, storleken på L det är:

L_i = m_ir_iv_i

Linjär hastighet v är relaterad till vinkelhastigheten ω genom:

v_i = r_iω

Därför:

L_i = m_ir_i (r_iω) = m_ir_i^tvåω

Den totala vinkelmomentet för snurra L är summan av vinkelmomentet för varje partikel:

L = (∑m_ir_i^två ) ω

∑ m_ir_i^två  är tröghetsmomentet I av toppen, då:

L= Jagω

Därför L Y ω har samma riktning och känsla, som visas i figur 7.

Referenser

1. Bauer, W. 2011. Fysik för teknik och vetenskap. Volym 1. Mc Graw Hill. 
2. Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 
3. Kirkpatrick, L. 2007. Fysik: En titt på världen. 6: e förkortade upplagan. Cengage Learning.
4. Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson. 
5. Serway, R., Jewett, J. (2008). Fysik för naturvetenskap och teknik. Volym 1 och 2. 7. Ed. Cengage Learning.