
Magnetiska motståndsenheter, formler, beräkning, exempel
De magnetisk motstånd eller magnetiskt motstånd är motsättningen som ett medium presenterar mot magnetflödets passage: ju högre motstånd, desto svårare är det att skapa magnetflödet. I en magnetisk krets har motvillighet samma roll som den elektriska resistansen i en elektrisk krets.
En spole som drivs av en elektrisk ström är ett exempel på en mycket enkel magnetisk krets. Tack vare strömmen genereras ett magnetiskt flöde som beror på spolens geometriska arrangemang och även på intensiteten hos strömmen som strömmar genom den..

Artikelindex
- 1 Formler och enheter
- 2 Hur beräknas magnetisk motstånd?
- 3 Skillnad med elektriskt motstånd
- 4 Exempel
- 4.1 Solenoider
- 4.2 Spollindad på en rektangulär järnkärna
- 5 Övningar lösta
- 5.1 - Övning 1
- 5.2 - Övning 2
- 6 Referenser
Formler och enheter
Betecknar magnetflödet som Φm, du har:
Φm = N.i / (ℓc / μAc)
Var:
-N är antalet varv hos spolen.
-Strömens intensitet är i.
-ℓc representerar längden på kretsen.
-TILLc är tvärsnittsområdet.
-μ är mediets permeabilitet.
Faktorn i nämnaren som kombinerar geometrin plus mediets inflytande är exakt kretsens magnetiska reluktans, en skalär kvantitet som betecknas med bokstaven ℜ, för att skilja den från det elektriska motståndet. A) Ja:
ℜ = ℓc / μ.Ac
I det internationella systemet för enheter (SI) mäts as som det inversa av henry (multiplicerat med antalet varv N). I sin tur är henry enheten för magnetisk induktans, motsvarande 1 tesla (T) x kvadratmeter / ampere. Därför:
1 TIMME-1 = 1 A / T.mtvå
Som 1 T.mtvå = 1 weber (Wb), motvilja uttrycks också i A / Wb (ampere / weber eller oftare ampere-turn / weber).
Hur beräknas magnetisk motstånd?
Eftersom magnetisk reluktans har samma roll som elektriskt motstånd i en magnetisk krets är det möjligt att utöka analogin med en ekvivalent av Ohms lag V = IR för dessa kretsar.
Även om det inte cirkulerar ordentligt, är det magnetiska flödet Φm tar platsen för strömmen, medan istället för spänning V, definierar magnetisk spänning eller magnetkraft, analog med elektromotorisk kraft eller till exempel i elektriska kretsar.
Magnetkraften är ansvarig för att upprätthålla det magnetiska flödet. Förkortad f.m.m och betecknas som ℱ. Med det har vi äntligen en ekvation som relaterar till de tre storheterna:
ℱ = Φm . ℜ
Och att jämföra med ekvationen Φm = N.i / (ℓc / μAc), det dras slutsatsen att:
ℱ = N.i
På detta sätt kan motviljan beräknas med vetskap om geometrin hos kretsen och mediets permeabilitet, eller också att känna till det magnetiska flödet och den magnetiska spänningen, tack vare denna sista ekvation, kallad Hopkinsons lag.
Skillnad med elektriskt motstånd
Ekvationen för magnetisk motstånd ℜ = ℓc / μAc liknar R = L / σA för elektriskt motstånd. I det senare representerar σ materialets konduktivitet, L är trådens längd och A är dess tvärsnittsarea.
Dessa tre kvantiteter: σ, L och A är konstanta. Emellertid permeabiliteten hos mediet μ, i allmänhet är den inte konstant, så att magnetkretsen hos en krets inte är konstant heller, till skillnad från dess elektriska likhet.
Om det sker en förändring i mediet, till exempel vid övergång från luft till järn eller tvärtom, sker en förändring i permeabilitet med den därmed varierande motviljan. Och även de magnetiska materialen går igenom hysterescykler.
Detta innebär att appliceringen av ett externt fält får materialet att behålla en del av magnetismen, även efter att fältet har tagits bort..
Av denna anledning är det nödvändigt att noggrant specificera vid vilken tidpunkt i cykeln materialet är beläget och därmed veta dess magnetisering varje gång den magnetiska motståndet beräknas..
Exempel
Även om motviljan beror mycket på kretsens geometri beror det också på mediets permeabilitet. Ju högre detta värde, desto lägre motvilja; så är fallet med ferromagnetiska material. Luft, å andra sidan, har låg permeabilitet, därför är dess magnetiska motstånd högre..
Solenoider
En solenoid är en lindning av längden ℓ gjorda med N-varv, genom vilka en elektrisk ström passerar I. Vändningarna lindas vanligtvis på ett cirkulärt sätt.
Inuti det genereras ett intensivt och enhetligt magnetfält, medan utanför fältet blir ungefär noll..
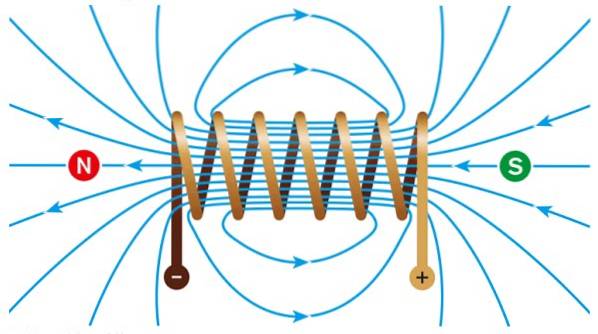
Om lindningen ges en cirkulär form finns det en torus. Inuti kan det finnas luft, men om en järnkärna placeras är magnetflödet mycket högre tack vare den höga permeabiliteten hos detta mineral.
Spole lindad på en rektangulär järnkärna
En magnetisk krets kan byggas genom att linda spolen på en rektangulär järnkärna. På detta sätt, när en ström passerar genom tråden, är det möjligt att upprätta ett intensivt fältflöde begränsat inuti järnkärnan, såsom visas i figur 3.
Motviljan beror på kretsens längd och tvärsnittsarean som anges i figuren. Den visade kretsen är homogen, eftersom kärnan är gjord av ett enda material och tvärsnittet förblir enhetligt..
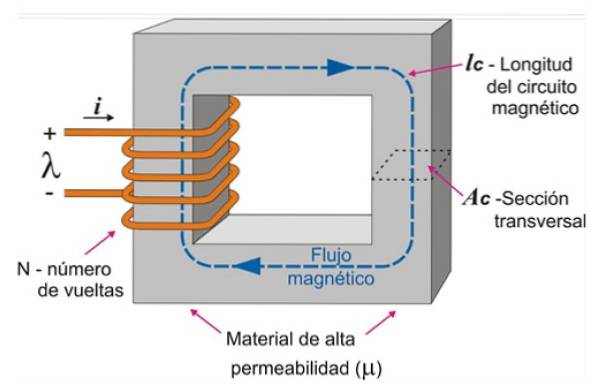
Lösta övningar
- Övning 1
Hitta magnetisk motstånd hos en raklinjig solenoid med 2000 varv, med vetskap om att när en ström av 5 A strömmar genom den genereras ett magnetiskt flöde på 8 mWb.
Lösning
Ekvationen används ℱ = N.i för att beräkna den magnetiska spänningen, eftersom strömens intensitet och antalet varv i spolen är tillgängliga. Det multiplicerar bara:
ℱ = 2000 x 5 A = 10 000 amp-varv
Sedan görs användning av ℱ = Φm . ℜ, var noga med att uttrycka det magnetiska flödet i weber (prefixet "m" betyder "milli", så det multipliceras med 10 -3:
Φm = 8 x 10 -3 Wb
Nu rensas motviljan och värdena ersätts:
ℜ = ℱ / Φm = 10.000 amp-turn / 8 x 10 -3 Wb = 1,25 x 106 amp-turn / Wb
- Övning 2
Beräkna kretsens magnetiska motstånd med figurerna med de visade måtten, som är i centimeter. Kärnans permeabilitet är μ = 0,005655 Tm / A och tvärsnittsarean är konstant, 25 cmtvå.
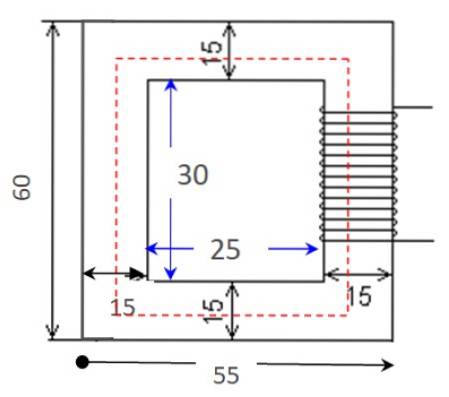
Lösning
Vi kommer att tillämpa formeln:
ℜ = ℓc / μAc
Permeabilitet och tvärsnittsarea finns som data i uttalandet. Det återstår att hitta längden på kretsen, som är omkretsen av den röda rektangeln i figuren.
För detta beräknas längden på en horisontell sida i genomsnitt, vilket adderar den större längden och den kortare längden: (55 +25 cm) / 2 = 40 cm. Fortsätt sedan på samma sätt för den vertikala sidan: (60 +30 cm) / 2 = 45 cm.
Slutligen läggs de genomsnittliga längderna på de fyra sidorna till:
ℓc = 2 x 40 cm + 2 x 45 cm = 170 cm
Subtrahera ersättningsvärden i motvillighetsformeln, men inte innan du uttrycker längden och arean av tvärsnittet - ges i uttalandet - i SI-enheter:
ℜ = 170 x 10 -tvåm / (0,005655 Tm / A x 0,0025 mtvå) = 120,248 amp-vrid / Wb
Referenser
- Alemán, M. Ferromagnetisk kärna. Återställd från: youtube.com.
- Magnetkrets och motvilja. Återställd från: mse.ndhu.edu.tw.
- Spinadel, E. 1982. Elektriska och magnetiska kretsar. Nytt bibliotek.
- Wikipedia. Magnetkraft. Återställd från: es.wikipedia.org.
- Wikipedia. Magnetisk motvilja. Återställd från: es.wikipedia.org.



Ingen har kommenterat den här artikeln än.