
Kvadratiska sekvenser exempel, regel och lösta övningar
De kvadratiska sekvenser, i matematiska termer består de av sekvenser av tal som följer en viss aritmetisk regel. Det är intressant att känna till denna regel för att bestämma villkoren i en sekvens.
Ett sätt att uppnå detta är att bestämma skillnaden mellan två på varandra följande termer och se om det erhållna värdet alltid upprepas. När så är fallet sägs det vara ett regelbunden arv.

Men om det inte upprepas kan du försöka undersöka skillnad mellan skillnader och se om detta värde är konstant. I så fall är det en kvadratisk sekvens.
Artikelindex
- 1 Exempel på vanliga och kvadratiska sekvenser
- 1.1 Exempel på regelbunden arv
- 1.2 Exempel på icke-regelbunden och kvadratisk sekvens
- 2 Allmän regel för att konstruera en kvadratisk sekvens
- 2.1 Skillnad mellan två på varandra följande termer av en kvadratisk sekvens
- 3 Lösta problem med kvadratiska sekvenser
- 3.1 Övning 1
- 3.2 Övning 2
- 3.3 Övning 3
- 4 Referenser
Exempel på vanliga och kvadratiska sekvenser
Följande exempel hjälper till att klargöra vad som har förklarats hittills:
Exempel på regelbunden arv
Låt sekvensen S = 4, 7, 10, 13, 16, ...
Denna sekvens, betecknad med S, är en oändlig numerisk uppsättning, i detta fall av heltal.
Det kan ses att det är en vanlig sekvens, eftersom varje term erhålls genom att lägga till 3 till föregående term eller element:
4
4 +3 = 7
7+3 = 10
10+3 = 13
13+3 = 16
Med andra ord: denna sekvens är regelbunden eftersom skillnaden mellan nästa term och den föregående ger ett fast värde. I det givna exemplet är detta värde 3.
De vanliga sekvenserna som erhålls genom att lägga till en fast kvantitet till föregående term kallas också aritmetiska framsteg. Och skillnaden - konstant - mellan på varandra följande termer kallas anledning och betecknas R.
Exempel på icke-regelbunden och kvadratisk sekvens
Se nu följande sekvens:
S = 2, 6, 12, 20, 30,….
När successiva skillnader beräknas erhålls följande värden:
6-2 = 4
12-6 = 6
20-12 = 8
30-20 = 10
Skillnaderna är inte konstanta, så det kan sägas att det är en INTE vanlig sekvens.
Men om vi betraktar skillnaden, har vi en annan sekvens, som kommer att betecknas som Sdiff:
Sdiff = 4, 6, 8, 10,….
Denna nya arv är en regelbunden arv, eftersom varje term erhålls genom att lägga till det fasta värdet R = 2 till den föregående. Därför kan vi bekräfta att S är kvadratisk sekvens.
Allmän regel för att konstruera en kvadratisk sekvens
Det finns en allmän formel för att konstruera en kvadratisk sekvens:
Tn = A ∙ ntvå + B ∙ n + C
I denna formel är Tn är termen för position n för sekvensen. A, B och C är fasta värden, medan n varierar en efter en, det vill säga 1, 2, 3, 4, ...
I sekvensen S i föregående exempel A = 1, B = 1 och C = 0. Därifrån följer att formeln som genererar alla termer är: Tn = ntvå + n
Nämligen:
T1 = 1två + 1 = 2
Ttvå = 2två + 2 = 6
T3 = 3två + 3 = 12
T5 = 5två + 5 = 30
Tn = ntvå + n
Skillnad mellan två på varandra följande termer i en kvadratisk sekvens
Tn + 1 - Tn = [A ∙ (n + 1)två + B ∙ (n + 1) + C] - [A ∙ ntvå + B ∙ n + C]
Att utveckla uttrycket genom enastående produkt är fortfarande:
Tn + 1 - Tn = A ∙ ntvå + A ∙ 2 ∙ n + A + B ∙ n + B + C - A ∙ ntvå - B ∙ n - C
Genom att förenkla det får du:
Tn + 1 - Tn = 2 ∙ A ∙ n + A + B
Detta är formeln som ger sekvensen av skillnaderna SDif som kan skrivas så här:
Difn = A ∙ (2n + 1) + B
Där klart nästa termin är 2 ∙ Ibland den föregående. Det vill säga förhållandet mellan sekvensen av skillnader Sdiff är: R = 2 ∙ A.
Löste problem med kvadratiska sekvenser
Övning 1
Låt sekvensen S = 1, 3, 7, 13, 21, .... Bestäm om:
i) Är det regelbundet eller inte?
ii) Är det kvadratiskt eller inte
iii) Det var kvadratisk, sekvensen av skillnader och deras förhållande
Svar
i) Låt oss beräkna skillnaden mellan följande och föregående termer:
3-1 = 2
7-3 = 4
13-7 = 6
21-13 = 8
Det kan vi bekräfta sekvensen S är inte regelbunden, eftersom skillnaden mellan på varandra följande termer inte är konstant.
ii) Skillnadssekvensen är regelbunden, eftersom skillnaden mellan dess termer är det konstanta värdet 2. Därför den ursprungliga sekvensen S är kvadratisk.
iii) Vi har redan bestämt att S är kvadratisk, skillnaden är:
Sdiff = 2, 4, 6, 8, ... och dess förhållande är R = 2.
Övning 2
Låt sekvensen S = 1, 3, 7, 13, 21, ... från föregående exempel, där det verifierades att den är kvadratisk. Bestämma:
i) Formeln som bestämmer den allmänna termen Tn .
ii) Kontrollera tredje och femte termerna.
iii) Värdet av den tionde termen.
Svar
i) Den allmänna formeln för Tn är A ∙ ntvå + B ∙ n + C. Då återstår att känna till värdena för A, B och C.
Förskjutningssekvensen har förhållande 2. Vidare är förhållandet R för varje kvadratisk sekvens 2 ∙ A som visas i föregående avsnitt.
R = 2 ∙ A = 2 vilket får oss att dra slutsatsen att A = 1.
Den första termen för sekvensen av skillnader SDif är 2 och måste uppfylla A ∙ (2n + 1) + B, med n = 1 och A = 1, det vill säga:
2 = 1 ∙ (2 ∙ 1 + 1) + B
lösa för B, får vi: B = -1
Då är den första termen S (n = 1) värd 1, det vill säga: 1 = A ∙ 1två + B ∙ 1 + C. Som vi redan vet att A = 1 och B = -1, ersätter vi:
1 = 1 ∙ 1två + (-1) ∙ 1 + C
Lösning för C får vi dess värde: C = 1.
Sammanfattningsvis:
A = 1, B = -1 och C = 1
Då blir den n: e termen Tn = ntvå - n + 1
ii) Den tredje termen T3 = 3två - 3 + 1 = 7 och det är verifierat. Den femte T5 = 5två - 5 + 1 = 21 som också verifieras.
iii) Den tionde terminen blir T10 = 10två - 10 + 1 = 91.
Övning 3
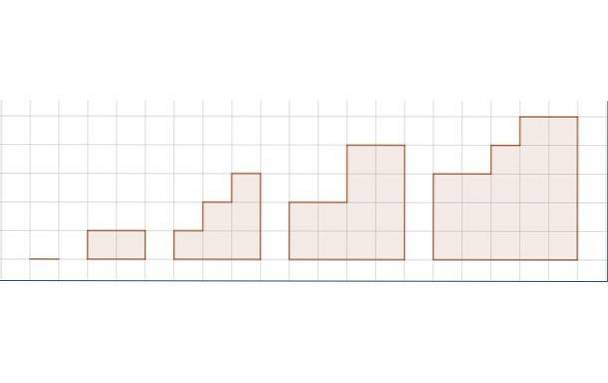
Figuren visar en sekvens av fem figurer. Gitteret representerar längdenheten.
i) Bestäm sekvensen för figurernas område.
ii) Visa att det är en kvadratisk sekvens.
iii) Hitta området i figur # 10 (visas inte).
Svar
i) Sekvensen S motsvarande området för figurens sekvens är:
S = 0, 2, 6, 12, 20,…
ii) Sekvensen som motsvarar de på varandra följande skillnaderna i termerna för S är:
Sdiff = 2, 4, 6, 8,…
Eftersom skillnaden mellan på varandra följande termer inte är konstant är S inte en vanlig sekvens. Det återstår att känna om det är kvadratiskt, för vilket vi återigen gör sekvensen av skillnaderna och erhåller:
2, 2, 2, ....
Eftersom alla termer i sekvensen upprepas bekräftas att S är en kvadratisk sekvens.
iii) Sekvensen Sdiff är regelbunden och dess förhållande R är 2. Med hjälp av ekvationen som visas ovan R = 2 ∙ A förblir den:
2 = 2 ∙ A, vilket innebär att A = 1.
Den andra termen för sekvensen av skillnader SDif är 4 och den n: e termen för SDif det är
A ∙ (2n + 1) + B.
Den andra termen har n = 2. Dessutom har det redan bestämts att A = 1, så med den tidigare ekvationen och ersättning har vi:
4 = 1 ∙ (2 ∙ 2 + 1) + B
Lösning för B får vi: B = -1.
Det är känt att den andra termen S är värd 2 och att den måste uppfylla formeln för den allmänna termen med n = 2:
Tn = A ∙ ntvå + B * n + C; n = 2; A = 1; B = -1; Ttvå = 2
Nämligen
2 = 1 ∙ 2två - 1 ∙ 2 + C
Man drar slutsatsen att C = 0, det vill säga att formeln som ger den allmänna termen för sekvensen S är:
Tn = 1 ∙ ntvå - 1 ∙ n +0 = ntvå - n
Nu är den femte termen verifierad:
T5 = 5två - 5 = 20
iii) Figur # 10, som inte har ritats här, kommer att ha det område som motsvarar den tionde termen för sekvensen S:
T10 = 10två - 10 = 90
Referenser
- https://www.geogebra.org



Ingen har kommenterat den här artikeln än.