De Bernoullis sats, som beskriver beteendet hos en vätska i rörelse, förklarades av matematikern och fysikern Daniel Bernoulli i sitt arbete Hydrodynamik. Enligt principen kommer en ideal vätska (utan friktion eller viskositet) som cirkulerar genom en sluten ledning att ha en konstant energi i sin väg.
Satsen kan härledas från principen om bevarande av energi och till och med från Newtons andra rörelselag. Dessutom fastställer Bernoullis princip också att en ökning av hastigheten hos en vätska innebär en minskning av trycket som den utsätts för, en minskning av dess potentiella energi eller båda samtidigt..
Satsen har många olika tillämpningar, både i vetenskapens värld och i människors vardag..
Dess konsekvenser finns i flygplanens lyftkraft, i skorstenar i hem och industrier, i vattenledningar, bland andra områden..
Artikelindex
Även om Bernoulli var den som drog slutsatsen att trycket minskar när flödeshastigheten ökar, är sanningen att det var Leonhard Euler som faktiskt utvecklade Bernoulli-ekvationen i den form som den är känd idag..
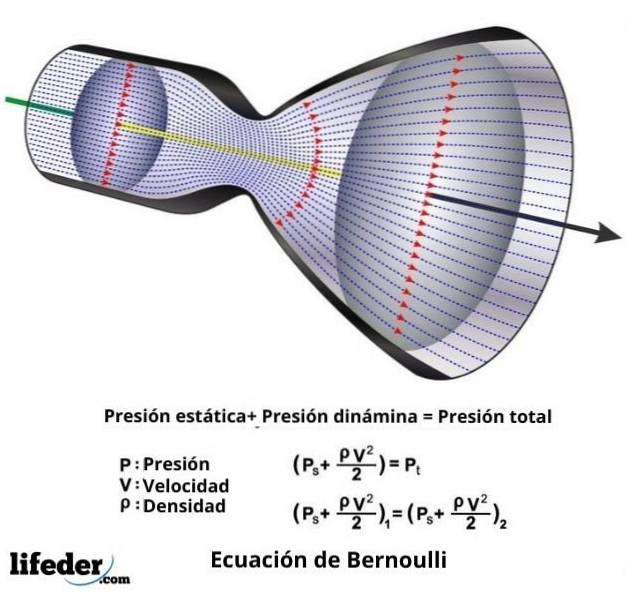
Hur som helst är Bernoullis ekvation, som inte är något annat än det matematiska uttrycket för hans sats, följande:
vtvå ∙ ƿ / 2 + P + ƿ ∙ g ∙ z = konstant
I detta uttryck är v hastigheten för vätskan genom den betraktade sektionen, ƿ är vätskans densitet, P är vätskans tryck, g är värdet av tyngdacceleration och z är höjden uppmätt i gravitationens riktning.
Det är implicit i Bernoullis ekvation att energin i en vätska består av tre komponenter:
- En kinetisk komponent, som är den som härrör från den hastighet med vilken vätskan rör sig.
- En potentiell eller gravitationskomponent, som beror på höjden vid vilken vätskan är.
- En tryckenergi, som är den som vätskan besitter som en följd av det tryck den utsätts för.
Å andra sidan kan Bernoullis ekvation också uttryckas så här:
v1 två ∙ ƿ / 2 + P1 + ƿ ∙ g ∙ z1 = vtvåtvå ∙ ƿ / 2 + Ptvå + ƿ ∙ g ∙ ztvå
Det sista uttrycket är mycket praktiskt för att analysera de förändringar som en vätska upplever när något av de element som utgör ekvationen ändras.
Vid vissa tillfällen är förändringen i ρgz-termen för Bernoullis ekvation minimal jämfört med den som de andra termerna upplever, så det kan försummas. Till exempel händer detta i strömmar som upplevs av ett flygplan under flygning..
Vid dessa tillfällen uttrycks Bernoullis ekvation enligt följande:
P + q = P0
I detta uttryck är q dynamiskt tryck och motsvarar v två ∙ ƿ / 2 och P0 är vad som kallas totaltryck och är summan av det statiska trycket P och det dynamiska trycket q.
Bernoullis teorem har många och olika tillämpningar inom områden så olika som vetenskap, teknik, sport, etc..
En intressant applikation finns i utformningen av eldstäder. Skorstenarna är byggda högt för att uppnå en större tryckskillnad mellan basen och skorstenens utlopp, tack vare vilket det är lättare att extrahera förbränningsgaserna.
Naturligtvis gäller Bernoullis ekvation också för studier av rörelsen av vätskeflöden i rör. Av ekvationen följer att en minskning av rörets tvärsnittsarea för att öka hastigheten för vätskan som passerar genom det också innebär en minskning av trycket.
Bernoulli-ekvationen används också i luftfart och i fordon i Formel 1. När det gäller luftfart är Bernoulli-effekten ursprunget till flygplanets lyft..
Flygplansvingar är utformade med målet att uppnå större luftflöde högst upp på vingen.
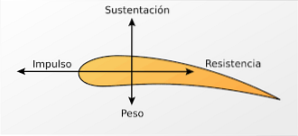
Sålunda är lufthastigheten i den övre delen av vingen hög och därför är trycket lägre. Denna tryckdifferens ger en vertikalt uppåt riktad kraft (lyftkraft) som gör att flygplanet kan sväva i luften. En liknande effekt erhålls i krängningsrullarna i Formel 1-bilar.
Genom ett rör med ett tvärsnitt på 4,2 cmtvå en ström av vatten strömmar vid 5,18 m / s. Vattnet sjunker från en höjd av 9,66 m till en lägre nivå med en höjd av noll höjd, medan rörets tvärsnittsarea ökar till 7,6 cmtvå.
a) Beräkna vattenströmmen på lägre nivå.
b) Bestäm trycket vid den nedre nivån med vetskap om att trycket vid den övre nivån är 152000 Pa.
a) Med tanke på att flödet måste bevaras är det sant att:
FÖvre nivån = Qlägre nivå
v1 . S1 = vtvå . Stvå
5,18 m / s. 4,2 cmtvå = vtvå . 7,6 cm ^två
Lösning för erhålls att:
vtvå = 2,86 m / s
b) Tillämpa Bernoullis sats mellan de två nivåerna och ta hänsyn till att vattentätheten är 1000 kg / m3 , det erhålls att:
v1 två ∙ ƿ / 2 + P1 + ƿ ∙ g ∙ z1 = vtvåtvå ∙ ƿ / 2 + Ptvå + ƿ ∙ g ∙ ztvå
(1/2). 1000 kg / m3 . (5,18 m / s)två + 152000 + 1000 kg / m3 . 10 m / stvå . 9,66 m =
= (1/2). 1000 kg / m3 . (2,86 m / s)två + Ptvå + 1000 kg / m3 . 10 m / stvå . 0 m
Lösning för Ptvå du får:
Ptvå = 257926,4 Pa
Ingen har kommenterat den här artikeln än.