
Bolzanos sats Förklaring, tillämpningar och övningar
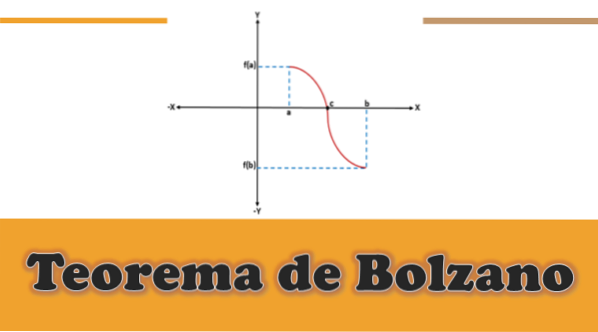
De Bolzano sats fastställer att om en funktion är kontinuerlig vid alla punkter i ett slutet intervall [a, b] och det är sant att bilden av "a" och "b" (under funktionen) har motsatta tecken, så kommer det att finnas minst en punkt "C" i det öppna intervallet (a, b), på ett sådant sätt att den funktion som utvärderas i "c" kommer att vara lika med 0.
Denna teorem förklarades av filosofen, teologen och matematikern Bernard Bolzano 1850. Denna forskare, född i dagens Tjeckien, var en av de första matematikerna i historien som gjorde ett formellt bevis på egenskaperna hos kontinuerliga funktioner..
Artikelindex
- 1 Förklaring
- 2 Demo
- 3 Vad är det för??
- 4 Lösta övningar
- 4.1 Övning 1
- 4.2 Övning 2
- 5 Referenser
Förklaring
Bolzanos teorem är också känd som teorem för mellanvärden, vilket hjälper till att bestämma specifika värden, särskilt nollor, för vissa verkliga funktioner hos en verklig variabel.
I en given funktion fortsätter f (x) - det vill säga att f (a) och f (b) är förbundna med en kurva-, där f (a) ligger under x-axeln (den är negativ), och f ( b) över x-axeln (den är positiv), eller vice versa, grafiskt kommer det att finnas en avskärningspunkt på x-axeln som representerar ett mellanliggande värde "c", som kommer att ligga mellan "a" och “B” och värdet på f (c) är lika med 0.
Genom att grafiskt analysera Bolzanos teorem kan man se att för varje kontinuerlig funktion f definierad i ett intervall [a, b], där f (a)*f (b) är mindre än 0, kommer det att finnas minst en rot "c" för den funktionen inom intervallet (a, b).
Denna sats fastställer inte antalet punkter i det öppna intervallet, det anger bara att det finns minst 1 poäng.
Demonstration
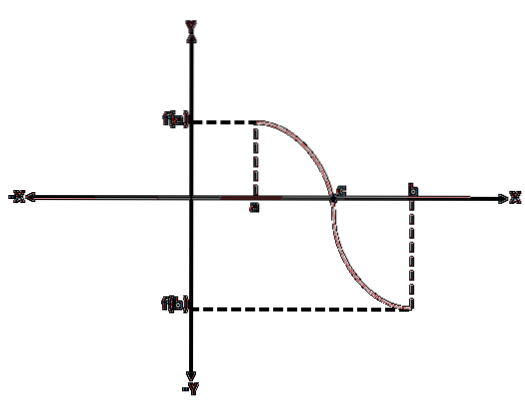
För att bevisa Bolzanos teorem antas det utan förlust av generalitet att f (a) < 0 y f(b) > 0; det kan alltså finnas många värden mellan "a" och "b" för vilka f (x) = 0, men det är bara nödvändigt att visa att det finns en.
Vi börjar med att utvärdera f vid mittpunkten (a + b) / 2. Om f ((a + b) / 2) = 0 så slutar beviset här; annars är f ((a + b) / 2) positiv eller negativ.
En av halvorna av intervallet [a, b] väljs så att tecknen på den funktion som utvärderas vid ytterpunkterna är olika. Detta nya intervall blir [a1, b1].
Nu, om f utvärderad vid mittpunkten för [a1, b1] inte är noll, utförs samma operation som tidigare; det vill säga att hälften av detta intervall väljs som uppfyller villkoren för tecknen. Låt detta nya intervall vara [a2, b2].
Om du fortsätter med den här processen kommer du att ha två sekvenser an och bn, så att:
an ökar och bn minskar:
a ≤ a1 ≤ a2 ≤… ≤ an ≤…. ≤…. ≤ bn ≤…. ≤ b2 ≤ b1 ≤ b.
Om längden på varje intervall [ai, bi] beräknas har vi:
bl-al = (b-a) / 2.
b2-a2 = (b-a) / 2².
... .
bn-an = (b-a) / 2 ^ n.
Därför är gränsen som n tenderar till oändligheten av (bn-an) lika med 0.
Att använda det att an ökar och begränsas och bn minskar och begränsas, vi har att det finns ett värde "c" så att:
a ≤ a1 ≤ a2 ≤… ≤ an ≤… .≤ c ≤…. ≤ bn ≤…. ≤ b2 ≤ b1 ≤ b.
Gränsen för a är "c" och gränsen för bn är också "c". Med tanke på vilket som helst δ> 0 finns det därför alltid ett "n" så att intervallet [an, bn] ingår i intervallet (c-δ, c + δ).
Nu måste det visas att f (c) = 0.
Om f (c)> 0, eftersom f är kontinuerlig, finns det en ε> 0 så att f är positiv över hela intervallet (c-ε, c + ε). Som sagt ovan finns det emellertid ett värde "n" så att f ändrar tecknet i [an, bn] och dessutom finns [an, bn] i (c-ε, c + ε), vilket är en motsägelse.
Om f (c) < 0, entonces como f es continua, existe un ε >O så att f är negativt under hela intervallet (c-e, c + e); men det finns ett värde "n" så att f ändrar tecken i [an, bn]. Det visar sig att [an, bn] ingår i (c-ε, c + ε), vilket också är en motsägelse.
Därför är f (c) = 0 och detta är vad vi ville visa.
Vad är det för?
Från sin grafiska tolkning används Bolzanos teorem för att hitta rötter eller nollor i en kontinuerlig funktion genom genomskärning (approximation), vilket är en inkrementell sökmetod som alltid delar intervallen med 2.
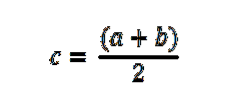
Därefter tas ett intervall [a, c] eller [c, b] där teckenförändringen inträffar och processen upprepas tills intervallet är mindre och mindre för att komma närmare det önskade värdet; det vill säga till det värde som funktionen gör 0.
Sammanfattningsvis, för att tillämpa Bolzanos teorem och därmed hitta rötterna, begränsa nollpunkterna för en funktion eller ge en lösning på en ekvation, utförs följande steg:
- Det verifieras om f är en kontinuerlig funktion på intervallet [a, b].
- Om intervallet inte anges måste man hitta där funktionen är kontinuerlig.
- Det verifieras om yttersta intervallet ger motsatta tecken när de utvärderas vid f.
- Om inga motsatta tecken uppnås måste intervallet delas in i två delintervaller med hjälp av mittpunkten.
- Utvärdera funktionen vid mittpunkten och verifiera att Bolzano-hypotesen är uppfylld, där f (a) * f (b) < 0.
- Beroende på tecknet (positivt eller negativt) på det hittade värdet upprepas processen med ett nytt delintervall tills den ovan nämnda hypotesen har uppfyllts..
Lösta övningar
Övning 1
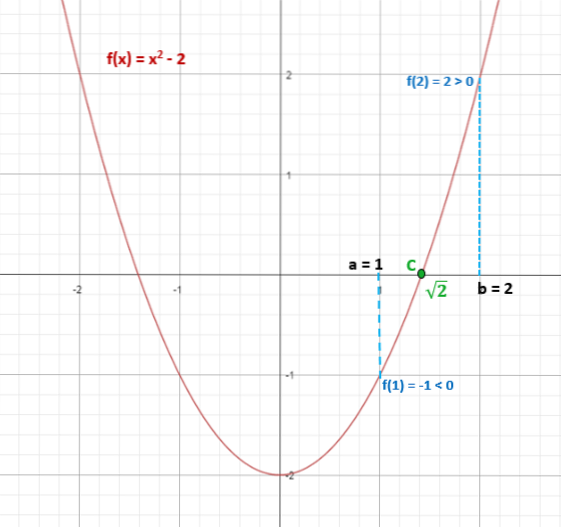
Bestäm om funktionen f (x) = xtvå - 2, har minst en verklig lösning i intervallet [1,2].
Lösning
Vi har funktionen f (x) = xtvå - 2. Eftersom det är polynom, betyder det att det är kontinuerligt i alla intervall.
Det ombeds att avgöra om det har en verklig lösning i intervallet [1, 2], så nu är det bara nödvändigt att ersätta ytterligheten av intervallet i funktionen för att känna till tecknet på dessa och veta om de uppfyller villkor att vara annorlunda:
f (x) = xtvå - två
f (1) = 1två - 2 = -1 (negativ)
f (2) = 2två - 2 = 2 (positivt)
Därför, tecken på f (1) ≠ tecken f (2).
Detta säkerställer att det finns minst en punkt "c" som tillhör intervallet [1,2], där f (c) = 0.
I detta fall kan värdet på "c" lätt beräknas enligt följande:
xtvå - 2 = 0
x = ± √2.
Således hör √2 ≈ 1,4 till intervallet [1,2] och uppfyller att f (√2) = 0.
Övning 2
Visa att ekvationen x5 + x + 1 = 0 har minst en riktig lösning.
Lösning
Låt oss först märka att f (x) = x5 + x + 1 är en polynomfunktion, vilket betyder att den är kontinuerlig på alla reella tal.
I det här fallet ges inget intervall, så värden måste väljas intuitivt, helst nära 0, för att utvärdera funktionen och hitta teckenförändringarna:
Om du använder intervallet [0, 1] måste du:
f (x) = x5 + x + 1.
f (0) = 05 + 0 + 1 = 1> 0.
f (1) = 15 + 1 + 1 = 3> 0.
Eftersom det inte finns någon teckenförändring upprepas processen med ett annat intervall.
Om du använder intervallet [-1, 0] måste du:
f (x) = x5 + x + 1.
f (-1) = (-1)5 + (-1) + 1 = -1 < 0.
f (0) = 05 + 0 + 1 = 1> 0.
I detta intervall finns en teckenförändring: tecken på f (-1) ≠ tecken på f (0), vilket betyder att funktionen f (x) = x5 + x + 1 har minst en verklig rot "c" i intervallet [-1, 0], så att f (c) = 0. Med andra ord är det sant att x5 + x + 1 = 0 har en verklig lösning i intervallet [-1,0].
Referenser
- Bronshtein I, S. K. (1988). Matematikhandbok för ingenjörer och studenter ... Redaktionellt MIR.
- George, A. (1994). Matematik och sinne. Oxford University Press.
- Ilín V, P. E. (1991). Matematisk analys. I tre volymer ...
- Jesús Gómez, F. G. (2003). Gymnasielärare. Volym II. GALEN.
- Mateos, M. L. (2013). Grundläggande egenskaper för analys i R. Editores, 20 dec.
- Piskunov, N. (1980). Differentiell och integrerad beräkning ...
- Sydsaeter K, H. P. (2005). Matematik för ekonomisk analys. Felix Varela.
- William H. Barker, R. H. (s.f.). Kontinuerlig symmetri: Från Euclid till Klein. American Mathematical Soc.



Ingen har kommenterat den här artikeln än.