
Euclids sats Bevis, tillämpning och övningar
De Euklids sats visar egenskaperna hos en rätt triangel genom att rita en linje som delar den i två nya högra trianglar som liknar varandra och i sin tur liknar den ursprungliga triangeln; då finns det ett förhållande av proportionalitet.
Euclid var en av de största matematikerna och geometrikerna i antiken som utförde flera bevis på viktiga satser. En av de viktigaste är den som bär hans namn, som har haft en bred tillämpning.

Detta har varit fallet eftersom det genom denna sats på ett enkelt sätt förklarar de geometriska förhållandena som finns i den högra triangeln, där benen på detta är relaterade till deras utsprång i hypotenusen..
Artikelindex
- 1 Formler och bevis
- 1.1 Höjdteorem
- 1.2 Benteorem
- 2 Förhållandet mellan Euklids satser
- 3 Lösta övningar
- 3.1 Exempel 1
- 3.2 Exempel 2
- 4 Referenser
Formler och demonstration
Euklids sats föreslår att i varje rätt triangel, när en linje dras - som representerar höjden som motsvarar toppunkten för den rätta vinkeln i förhållande till hypotenusen - bildas två högra trianglar från original.
Dessa trianglar kommer att likna varandra och kommer också att likna den ursprungliga triangeln, vilket innebär att deras liknande sidor är proportionella mot varandra:
De tre trianglarnas vinklar är kongruenta; det vill säga när de roteras 180 grader kring sin topp, sammanfaller en vinkel med den andra. Detta innebär att de alla kommer att vara desamma.
På detta sätt kan likheten som finns mellan de tre trianglarna också verifieras genom att deras vinklar är lika. Från likheten mellan trianglar, fastställer Euclid proportionerna av dessa från två satser:
- Höjdteorem.
- Benteorem.
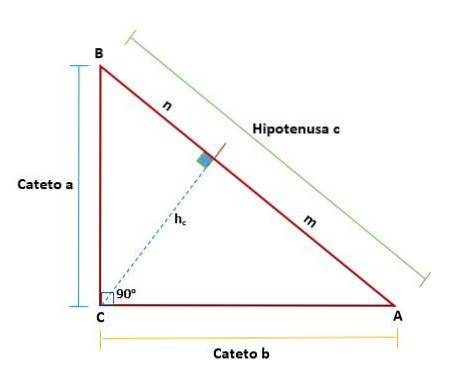
Denna teorem har en bred tillämpning. I antiken användes den för att beräkna höjder eller avstånd, vilket representerar ett stort framsteg för trigonometri.
Det används för närvarande inom olika områden som är baserade på matematik, såsom teknik, fysik, kemi och astronomi, bland många andra områden..
Höjdteorem
I denna sats fastställs att i vilken rätt triangel som helst är höjden som dras från rätt vinkel med avseende på hypotenusen det geometriska proportionella medelvärdet (kvadraten på höjden) mellan benprojektionerna som den bestämmer på hypotenuse.
Det vill säga höjdens kvadrat kommer att vara lika med multiplikationen av de projicerade benen som bildar hypotenusen:
hctvå = m * n
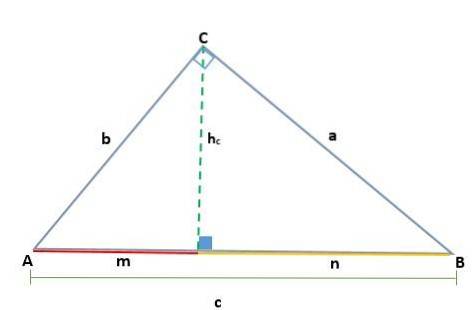
Demonstration
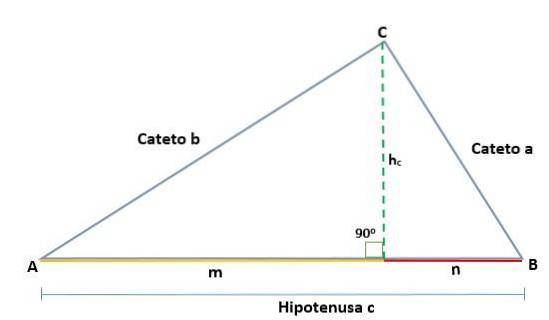
Med tanke på en triangel ABC, som ligger precis vid toppunkt C, genererar planering av höjden två liknande högra trianglar, ADC och BCD; därför är deras motsvarande sidor proportionella:
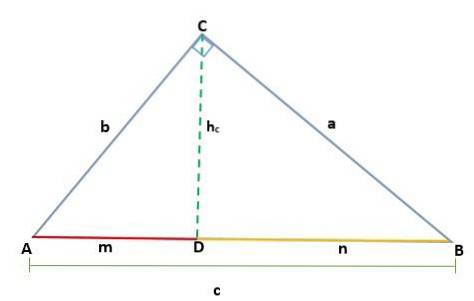
På ett sådant sätt att höjden hc som motsvarar segmentet CD, motsvarar hypotenusen AB = c, så vi har:
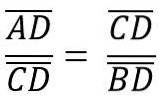
I sin tur motsvarar detta:
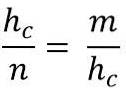
Lösning för hypotenusen (hc), för att multiplicera de två jämställdhetsmedlemmarna måste vi:
hc * hc = m * n
hctvå = m * n
Sålunda ges värdet av hypotenusen av:
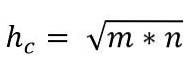
Benteorem
I denna sats fastställs att måttet på varje ben i varje rätt triangel är det geometriska proportionella medelvärdet (kvadratet på varje ben) mellan måttet på hypotenusen (komplett) och projektionen av var och en på den:
btvå = c * m
tilltvå = c* n
Demonstration
Med tanke på en triangel ABC, som är precis vid toppunkten C, på ett sådant sätt att dess hypotenus är c, vid planering av höjden (h) bestäms utsprången för benen a och b, vilka är segmenten m respektive n, och som ligger på hypotenus.
Således har vi att höjden ritad på höger triangel ABC genererar två liknande högra trianglar, ADC och BCD, så att motsvarande sidor är proportionella, så här:
DB = n, vilket är projektionen av ben CB på hypotenusen.
AD = m, vilket är projektionen av benet AC på hypotenusen.
Därefter bestäms hypotenusen c av summan av benen på dess utsprång:
c = m + n
På grund av likheten mellan trianglarna ADC och BCD har vi:
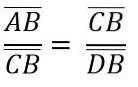
Ovanstående är samma som:
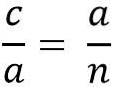
Lösning för ben "a" för att multiplicera de två medlemmarna av jämställdheten, vi har:
till * a = c * n
tilltvå = c * n
Värdet på ben "a" ges således av:
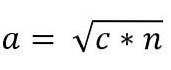
På samma sätt, på grund av likheten mellan trianglarna ACB och ADC, har vi:
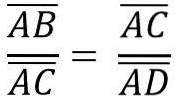
Ovanstående är lika med:
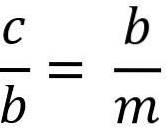
Lösning för ben "b" för att multiplicera de två medlemmarna av jämställdheten, vi har:
b * b = c * m
btvå = c * m
Således ges värdet på ben "b" av:
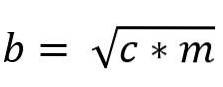
Förhållandet mellan Euklids teoremer
Satser med hänvisning till höjden och benen är relaterade till varandra eftersom måttet på båda är gjorda med avseende på hypotenusen i rätt triangel.
Genom förhållandet mellan Euklids teorem kan höjdens värde också hittas; detta är möjligt genom att lösa värdena på m och n från bensatsen och de ersätts i höjdsatsen. På detta sätt är det tillfredsställt att höjden är lika med multiplikationen av benen, dividerat med hypotenusen:
btvå = c * m
m = btvå ÷ c
tilltvå = c * n
n = atvå ÷ c
I höjdsatsen ersätter vi m och n:
hctvå = m * n
hctvå = (btvå ÷ c) * (tilltvå ÷ c)
hc = (btvå * tilltvå) ÷ c
Lösta övningar
Exempel 1
Med tanke på triangeln ABC, precis vid A, bestäm mätningen av AC och AD, om AB = 30 cm och BD = 18 cm
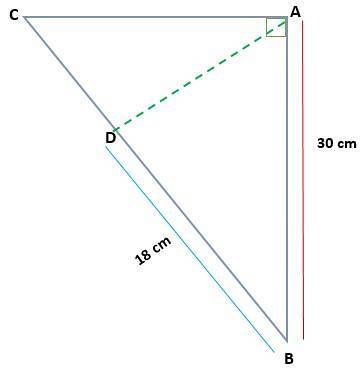
Lösning
I det här fallet har vi måtten på ett av de projicerade benen (BD) och ett av benen i den ursprungliga triangeln (AB). På detta sätt kan bensatsen tillämpas för att hitta värdet av benet BC.
ABtvå = BD * före Kristus
(30)två = 18 * före Kristus
900 = 18 * före Kristus
BC = 900 ÷ 18
BC = 50 cm
Värdet på ben-CD kan hittas med vetskap om att BC = 50:
CD = BC - BD
CD = 50 - 18 = 32 cm
Nu är det möjligt att bestämma värdet på benet AC genom att använda bensatsen igen:
ACtvå = CD * BD
ACtvå = 32 * femtio
ACtvå = 160
AC = √1600 = 40 cm
För att bestämma värdet på höjden (AD) tillämpas höjdsatsen, eftersom värdena på de projicerade benen CD och BD är kända:
ADtvå = 32 * 18
ADtvå = 576
AD = √576
AD = 24 cm
Exempel 2
Bestäm värdet på höjden (h) för en triangel MNL, precis i N, med kännedom om segmentens mått:
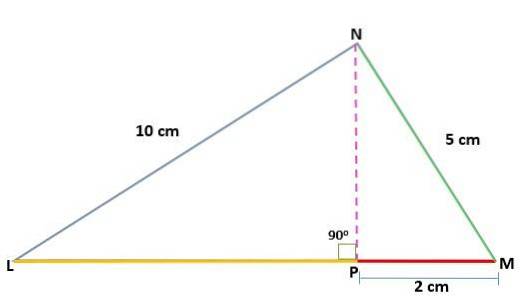
NL = 10 cm
MN = 5 cm
PM = 2 cm
Lösning
Vi har måttet på ett av benen projicerat på hypotenusen (PM), liksom måtten på benen i den ursprungliga triangeln. På detta sätt kan bensatsen användas för att hitta värdet av det andra projicerade benet (LN):
NLtvå = PM * LM
(10)två = 5 * LM
100 = 5 * LM
PL = 100 ÷ 5 = 20
Eftersom värdet på benen och hypotenusen redan är känd, genom förhållandet mellan höjdens och benens satser, kan värdet på höjden bestämmas:
NL = 10
MN = 5
LM = 20
h = (btvå * tilltvå) ÷ c.
h = (10två * 5två) ÷ (tjugo)
h = (100 * 25) ÷ (tjugo)
h = 2500 ÷ tjugo
h = 125 cm.
Referenser
- Braun, E. (2011). Kaos, fraktaler och konstiga saker. Fonden för ekonomisk kultur.
- Cabrera, V. M. (1974). Modern matematik, Volym 3.
- Daniel Hernandez, D. P. (2014). 3: e års matte. Caracas: Santillana.
- Encyclopaedia Britannica, i. (nittonhundranittiofem). Hispanic Encyclopedia: Macropedia. Encyclopedia Britannica Publishers.
- Euclid, R. P. (1886). Euclids element för geometri.
- Guardeño, A. J. (2000). Arvet från matematik: från Euclid till Newton, genierna genom sina böcker. Sevilla universitet.


Ingen har kommenterat den här artikeln än.