
Existens- och unikhetssats bevis, exempel och övningar
De Sats för existens och unikhet fastställer de nödvändiga och tillräckliga villkoren så att en första ordningens differentiella ekvation med ett givet initialt tillstånd har en lösning och att denna lösning också är den enda.
Satsen ger dock ingen teknik eller indikation på hur man hittar en sådan lösning. Satsen för existens och unikhet utvidgas också till högre ordningens differentiella ekvationer med initiala förhållanden, vilket är känt som Cauchy-problemet..
Det formella uttalandet om existens- och unikhetssatsen är som följer:
"För en differentiell ekvation y '(x) = f (x, y) med ursprungligt tillstånd y (a) = b, existerar åtminstone en lösning i ett rektangulärt område av planet XY innehåller till punkten (a, b), Ja f (x, y) det är kontinuerligt i den regionen. Och om det delvisa derivatet av F med tanke på Y: g = ∂f / ∂och är kontinuerlig i samma rektangulära område, då är lösningen unik i närheten av punkten (a, b) innehåll i kontinuitetsregionen F Y g."
Nyttan med denna sats ligger först i att veta vilka regioner i XY-planet där en lösning kan existera och också att veta om den lösning som hittats är den enda möjliga eller om det finns andra..
Observera att om unikt villkor inte är uppfyllt kan satsen inte förutsäga hur många lösningar totalt Cauchy-problemet har: kanske är det en, två eller fler.
Artikelindex
- 1 Bevis på existensen och unikhetssatsen
- 2 Exempel
- 2.1 - Exempel 1
- 2.2 - Exempel 2
- 3 Lösta övningar
- 3.1 - Övning 1
- 3.2 - Övning 2
- 4 Referenser
Bevis på existensen och unikhetssatsen

För denna sats är två möjliga bevis kända, en av dem är beviset för Charles Émile Picard (1856-1941) och den andra beror på Giuseppe Peano (1858-1932) baserat på verk av Augustin Louis Cauchy (1789-1857 ).
Det är anmärkningsvärt att de mest lysande matematiska hjärnorna på 1800-talet deltog i beviset på denna sats, så det kan antas att ingen av de två är enkel.
För att formellt bevisa satsen är det nödvändigt att först upprätta en serie mer avancerade matematiska begrepp, såsom Lipschitz-typfunktioner, Banach-utrymmen, Carathéodorys existenssats och flera andra, som ligger utanför artikelns räckvidd..
En stor del av de differentiella ekvationerna som hanteras i fysiken handlar om kontinuerliga funktioner i intressanta regioner, därför begränsar vi oss till att visa hur satsen tillämpas i enkla ekvationer.
Exempel
- Exempel 1
Låt oss överväga följande differentialekvation med ett initialt tillstånd:
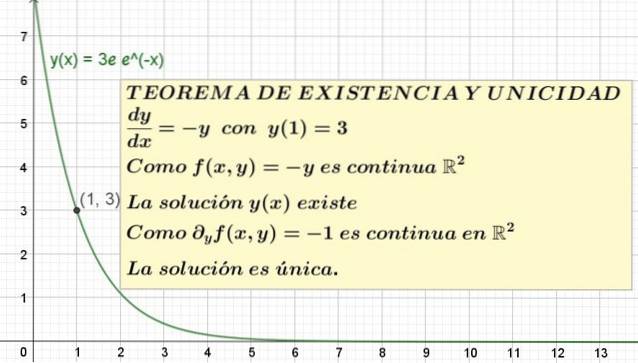
y '(x) = - y; med y (1) = 3
Finns det en lösning på detta problem? Är det den enda möjliga lösningen?
Svar
För det första utvärderas förekomsten av lösningen av differentialekvationen och att den också uppfyller det ursprungliga villkoret.
I detta exempel f (x, y) = - y förutsättningen för existens kräver att man vet om f (x, y) är kontinuerlig i ett område av planet XY som innehåller koordinatpunkten x = 1, y = 3.
Men f (x, y) = - y är affin funktion, som är kontinuerligt inom realtalsdomänen och existerar i hela intervallet av reella tal.
Därför dras slutsatsen att f (x, y) är kontinuerlig i Rtvå, så satsen garanterar att det finns minst en lösning.
Att veta detta är det nödvändigt att utvärdera om lösningen är unik eller om det tvärtom finns mer än en. För detta är det nödvändigt att beräkna delderivatet av F med avseende på variabeln Y:
∂f / ∂y = ∂ (-y) / ∂y = -1
Sedan g (x, y) = -1 vilket är en konstant funktion, som också definieras för alla Rtvå och det är också kontinuerligt där. Härav följer att existens- och unikhetssatsen garanterar att detta initialvärde-problem har en unik lösning, även om det inte säger oss vad det är..
- Exempel 2
Tänk på följande första ordningens ordinarie differentiella ekvation med startvillkor:
y '(x) = 2√y; y (0) = 0.
Finns det en lösning y (x) för detta problem? Om så är fallet, avgöra om det finns en eller flera.
Svar
Vi betraktar funktionen f (x, y) = 2√y. Funktionen F definieras endast för y≥0, eftersom vi vet att ett negativt tal saknar en riktig rot. Vad mer f (x, y) är kontinuerligt i det övre halva planet av Rtvå inklusive X-axeln, så satsen om existens och unikhet garanterar åtminstone en lösning i den regionen.
Nu är det initiala villkoret x = 0, y = 0 på kanten av lösningsområdet. Sedan tar vi det partiella derivatet av f (x, y) med avseende på y:
.F/ ∂y = 1 / √y
I det här fallet definieras inte funktionen för y = 0, exakt där det ursprungliga tillståndet är.
Vad säger satsen oss? Det berättar för oss att även om vi vet att det finns minst en lösning, det övre halva planet av X-axeln inklusive X-axeln, eftersom det unika villkoret inte är uppfyllt, finns det ingen garanti för att det kommer att finnas en unik lösning.
Det betyder att det kan finnas en eller flera lösningar i kontinuitetsregionen för f (x, y). Och som alltid berättar satsen oss inte vad de kan vara.
Lösta övningar
- Övning 1
Lös Cauchy-problemet i exempel 1:
y '(x) = - y; med y (1) = 3.
Hitta funktionen y (x) som uppfyller differentialekvationen och det initiala tillståndet.
Lösning
I exempel 1 bestämdes att detta problem har en lösning och också är unikt. För att hitta lösningen är det första att notera att det är en differentiell ekvation av den första graden av separerbara variabler, som skrivs enligt följande:
dy / dx = - y → dy = -y dx
Att dela mellan och i båda medlemmarna för att separera de variabler som vi har:
dy / y = - dx
Den obestämda integralen tillämpas i båda medlemmarna:
∫ (1 / y) dy = - ∫dx
Lösa de obestämda integralerna vi har:
ln (y) = -x + C.
där C är en konstant integration som bestäms av det ursprungliga tillståndet:
ln (3) = -1 + C, det vill säga C = 1 + ln (3)
Att ersätta C-värdet och ordna om det kvarstår:
ln (y) - ln (3) = -x + 1
Tillämpar följande logaritmegenskaper:
Skillnaden mellan logaritmer är kvotens logaritm
Ovanstående uttryck kan skrivas om så här:
ln (y / 3) = 1 - x
Den exponentiella funktionen med bas e i båda medlemmarna tillämpas för att erhålla:
y / 3 = e(1 - x)
Vilket motsvarar:
y = 3e e-x
Detta är den unika lösningen av ekvationen y '= -y med y (1) = 3. Grafen för denna lösning visas i figur 1.
- Övning 2
Hitta två lösningar för problemet i exempel 2:
y '(x) = 2√ (y); y (0) = 0.
Lösning
Det är också en ekvation av separerbara variabler, som, skrivna i differentiell form, ser ut så här:
dy / √ (y) = 2 dx
Att ta den obestämda integralen i båda medlemmarna kvarstår:
två √ (y) = 2 x + C.
Hur vet du det y≥0 i lösningsregionen har vi:
y = (x + C)två
Men eftersom det initiala villkoret x = 0, y = 0 måste uppfyllas, är konstanten C noll och följande lösning kvarstår:
y (x) = xtvå.
Men den här lösningen är inte unik, funktionen y (x) = 0 är också en lösning på det uppkomna problemet. Existens- och unikhetssatsen som tillämpades på detta problem i exempel 2 hade redan förutsagt att det kunde finnas mer än en lösning.
Referenser
- Coddington, Earl A.; Levinson, Norman (1955), Theory of Ordinary Differential Equations, New York: McGraw-Hill.
- Encyclopedia of Mathematics. Sats om Cauchy-Lipschitz. Återställd från: encyclopediaofmath.org
- Lindelöf, Sur l'application de la méthode des approximations successives aux équations différentielles ordinaires du premier ordre; Comptes rendus hebdomadaires des séances de l'Académie des sciences. Vol. 116, 1894, sid. 454-457. Återställd från: gallica.bnf.fr.
- Wikipedia. Picards successiva approximationsmetod. Återställd från: es.wikipedia.com
- Wikipedia. Sats Picard-Lindelöf. Återställd från: es.wikipedia.com.
- Zill, D. 1986. Elementära differentiella ekvationer med applikationer. Lärlingshall.

Ingen har kommenterat den här artikeln än.