Vertikala skottformler, ekvationer, exempel

De vertikalt skott Det är en rörelse som äger rum under inverkan av ett kraftfält, vanligtvis med tyngdkraften, och som kan gå uppåt eller nedåt. Det är också känt under namnet vertikal lansering.

Det mest omedelbara exemplet är att kasta upp (eller ner om du föredrar) en boll med handen, naturligtvis, se till att göra det i vertikal riktning. Bortsett från luftmotstånd passar rörelsen som bollen följer perfekt till modellen Uniformly Varied Rectilinear Motion (MRUV)..

Det vertikala skottet är en rörelse som studeras allmänt i introduktionskurser i fysik, eftersom det är ett urval av rörelse i en dimension, en mycket enkel och användbar modell.

Denna modell kan inte bara användas för att studera kinematiken för föremål under tyngdkraftsverkan, men också, som kommer att ses senare, beskriver rörelsen av partiklar mitt i ett enhetligt elektriskt fält..

Artikelindex

• 1 Formler och ekvationer
  • 1.1 Vertikala kastekvationer
• 2 Exempel
  • 2.1 Arbetat exempel 1
  • 2.2 Arbetat exempel 2
• 3 Referenser

Formler och ekvationer

Det första som behövs är ett koordinatsystem för att ange ursprunget och märka det med en bokstav, som i fallet med vertikala rörelser är bokstaven "Y".

Sedan väljs den positiva riktningen +Y, vilket vanligtvis är uppåt och känslan -Y som vanligtvis tas ner (se figur 2). Allt detta såvida inte problemlösaren bestämmer något annat, eftersom ett annat alternativ är att ta riktningen på rörelsen som positiv, oavsett vilken det kan vara..

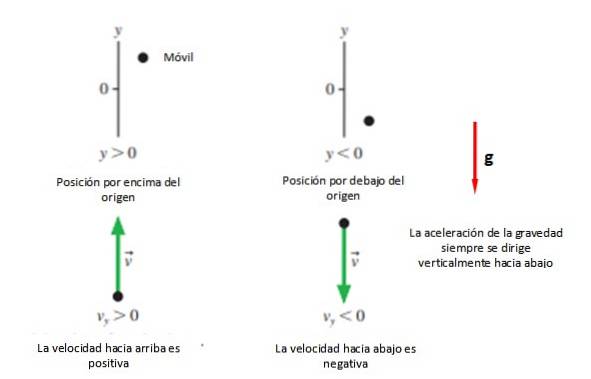
I vilket fall som helst rekommenderas att ursprunget sammanfaller med startpunkten. Y_eller, för på så sätt förenklas ekvationerna, även om du kan ta vilken position du vill för att börja studera rörelsen.

Vertikala kastekvationer

När vi väl har etablerat koordinatsystemet och ursprunget går vi till ekvationerna. De magnituder som beskriver rörelsen är:

-Ursprungliga hastigheten v_eller

-Acceleration till

-Hastighet v

-Första position x_eller

-Placera x

-Förflyttning Dx

-Väder t

Allt utom tid är vektorer, men eftersom det är en endimensionell rörelse med en viss riktning, är det viktigt då att använda + eller - tecken för att ange vart storleken i fråga går. När det gäller vertikalt drag, går tyngdkraften alltid nedåt och, om inte annat anges, tilldelas det ett tecken -.

Följande är ekvationerna anpassade för vertikalt drag, som ersätter “x" för "Y"Y"till" för "g”. Dessutom kommer skylten (-) som motsvarar gravitationen riktad nedåt att inkluderas på en gång:

1) Position: y = y_eller + v_eller.t - ½ g.t^två

2) Hastighet: v = v_eller - g.t

3) Hastighet som en funktion av förskjutning ΔY: v^två = v_eller^två - 2 g. ΔY

Exempel

Nedan följer applikationsexempel för vertikal fotografering. I sin resolution måste följande beaktas:

-"g”Har ett konstant värde som i genomsnitt är 9,8 m / s^två eller cirka 10 m / s^två om det föredras för att underlätta beräkningar när för mycket precision inte krävs.

-När v_eller Okej 0, dessa ekvationer minskar till de av fritt fall.

-Om lanseringen är uppåt måste objektet ha en initial hastighet som gör att den kan röra sig. En gång i rörelse når objektet en maximal höjd som beror på hur stor starthastigheten är. Naturligtvis, ju högre höjd, desto mer tid kommer mobilen att spendera i luften.

-Objektet återvänder till startpunkten med samma hastighet som det kastades med, men hastigheten riktas nedåt.

-För en vertikal start nedåt, ju högre initialhastighet, desto snabbare kommer objektet att träffa marken. Här ställs sträckan in i enlighet med höjden som valts för lanseringen.

-I det vertikala kastet uppåt beräknas den tid det tar för mobilen att nå maximal höjd genom att göra v = 0 i ekvation 2) i föregående avsnitt. Det här är maximal tid t_max:

0 = v_eller - g. t_max ⇒ t_max = v_eller / g

-De maxhöjd Y_max rensas från ekvation 3) i föregående avsnitt genom att göra detsamma v = 0:

0 = v_eller^två - 2 g. Δy ⇒ 0 = v_eller^två - 2 g. (Y_max - Y_eller) ⇒ och_max = och_eller  + v_eller^två / 2 g

Ja Y_eller = 0, Det reduceras till:

Y_max = v_eller^två / 2 g

Fungerat exempel 1

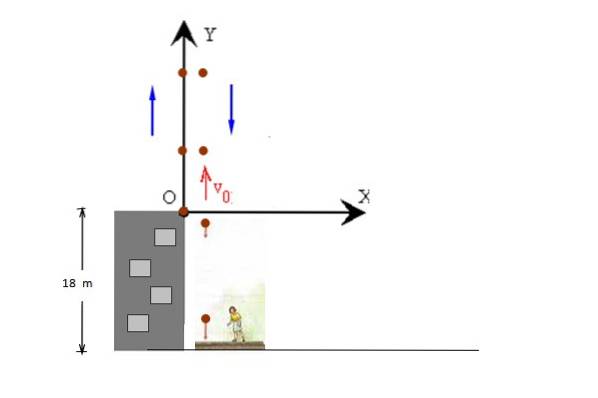
En boll kastas vertikalt uppåt med v_eller = 14 m / s, från toppen av en 18 m hög byggnad. Bollen får fortsätta vägen ner till trottoaren. Beräkna:

a) Bollens maximala höjd i förhållande till marken.

b) Den tid det var i luften (flygtid).

Lösning

Figuren visar höjning och sänkning av kulan separat för tydlighetens skull, men båda sker längs samma linje. Startpositionen tas vid y = 0, så att slutpositionen är y = - 18 m.

a) Den maximala höjden uppmätt från byggnadens tak är Y_max = v_eller^två / 2 g och från uttalandet kan vi läsa att initialhastigheten är +14 m / s, sedan:

Y_max = (14 m / s)^två / 2 x 9,8 m / s^två = 10 m (När det gäller taket)

H_max = 10 m + 18 m = 28 m (När det gäller trottoaren).

b) För att hitta total tid eller flygtid bollen håller i luften kommer ekvationen att användas y = y_eller + v_eller.t - ½ g.t^två, med följande värden och tecken:

y = - 18 m

Y_eller = 0 m

v_eller = +14 m / s

Ersätter:

- 18 = 14.t - ½ 9.8 .t^två

- 4,9 t^två+14.t + 18 = 0 

4,9 t^två-14.t - 18 = 0

Det är en ekvation av andra graden som lätt kan lösas med hjälp av en vetenskaplig miniräknare eller med hjälp av lösaren. Lösningarna är: 3.82 och -0.96. Den negativa lösningen kasseras eftersom det saknar fysisk förnuft eftersom det är en tid.

Flygtiden för bollen är 3,82 sekunder.

Fungerat exempel 2

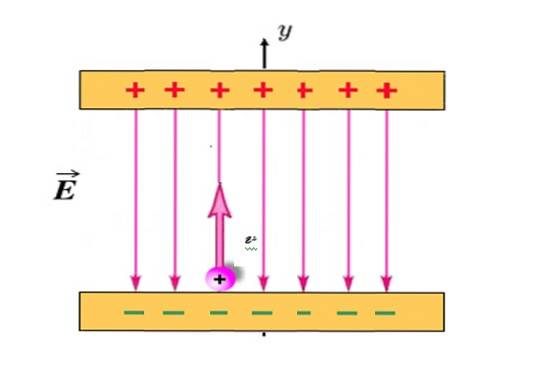
En positivt laddad partikel med q = +1,2 millicoulombs (mC) och massa m = 2,3 x 10 ^-10 Kg projiceras vertikalt uppåt, från det läge som visas i figuren och med initialhastighet v_eller = 30 km / s.

Mellan de laddade plattorna finns ett elektriskt fält OCH enhetlig, riktad vertikalt nedåt och med magnituden 780 N / C. Om avståndet mellan plattorna är 18 cm, kommer partikeln att kollidera med topplattan? Försumma gravitationens attraktion på partikeln, eftersom den är extremt lätt.

Lösning

I detta problem det elektriska fältet OCH är den som producerar en kraft F och därav följande acceleration. Eftersom partikeln är positivt laddad, lockas partikeln alltid till den nedre plattan, men när den projiceras vertikalt uppåt når den en maximal höjd och återgår sedan till den nedre plattan, precis som kulan i föregående exempel..

Per definition av elektriskt fält:

E = F / q = m.a / q ⇒ a = q.E / m

Du måste använda denna likvärdighet innan du ersätter värden:

1 mC = 1 x 10^-3 C

Således är accelerationen:

a = 1,2 x 10^-3 x 780 / 2,3 x 10 ^-10Fröken^två = 4,07 x 10⁹ Fröken^två

För maximal höjd används formeln från föregående avsnitt, men istället för att använda “g”Detta accelerationsvärde används:

Y_max = v_eller^två / 2a = (30000 m / s)^två/ 2 x 4,07 x 10⁹ Fröken^två = 0,11 m = 11 cm

Den kolliderar inte med den övre plattan, eftersom den är 18 cm från startpunkten och partikeln når bara 11 cm.

Referenser

1. Kirkpatrick, L. 2007. Fysik: En titt på världen. 6^ta Förkortad upplaga. Cengage Learning. 23 - 27.
2. Rex, A. 2011. Grundläggande fysik. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14^th. Utg. Volym 1. 50 - 53.
4. Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9^na Ed. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Fysik 10. Pearson Education. 133 - 149.