
Rätt trapetsegenskaper, förhållanden och formler, exempel
A rektangel trapes är en platt figur med fyra sidor, så att två av dem är parallella med varandra, kallade baser och en av de andra sidorna är vinkelrät mot baserna.
Av denna anledning är två av de inre vinklarna rätta, det vill säga de mäter 90º. Därav namnet "rektangel" som ges till figuren. Följande bild av en höger trapesform klargör dessa egenskaper:
Artikelindex
- 1 Element av trapezoid
- 2 Relationer och formler
- 2.1 Trapesens höjd h
- 2.2 Omkrets P
- 2.3 Genomsnittlig bas
- 2.4 Område
- 2.5 Diagonaler, sidor och vinklar
- 3 Exempel på rätt trapezoider
- 3.1 Trapesformen som designelement
- 3.2 Trapesformad våggenerator
- 3.3 I numerisk beräkning
- 3.4 Stråle med trapesformad belastning
- 3.5 Som ett pedagogiskt och lärande verktyg
- 4 Lösta övningar
- 4.1 - Övning 1
- 4.2 - Övning 2
- 5 Referenser
Element av trapetsformen
Elementen i trapezoid är:
-Baser
-Hörn
-Höjd
-Inre vinklar
-Mellersta bas
-Diagonaler
Vi kommer att detaljera dessa element med hjälp av figurerna 1 och 2:
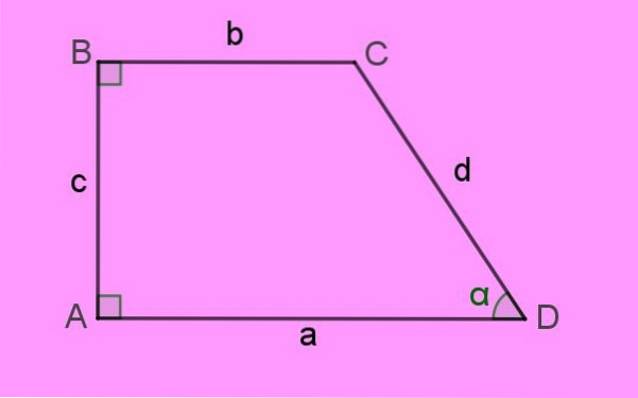
Sidorna på den högra trapesformen betecknas med små bokstäver a, b, c och d. Figurens hörn o hörn De anges med stora bokstäver. Slutligen inre vinklar De uttrycks i grekiska bokstäver.
Per definition, baser av denna trapets är sidorna a och b, som, som man kan se, är parallella och också har olika längder.
Sidan vinkelrätt mot båda baserna är sidan c till vänster, vilket är höjd h av trapetsen. Och slutligen finns sidan d som bildar den spetsiga vinkeln a med sidan a.
Summan av inre vinklar av en fyrkant är 360º. Det är lätt att förstå att den saknade vinkeln C i figuren är 180 - α.
De mitten bas är segmentet som sammanfogar mittpunkterna för de icke-parallella sidorna (segment EF i figur 2).
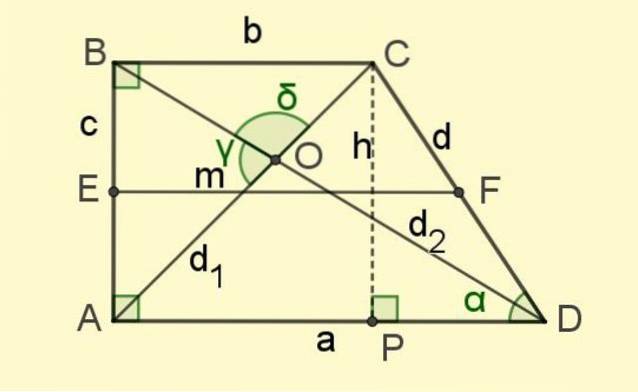
Och slutligen finns det diagonalerna d1 och dtvå, segmenten som förenar motsatta hörn och skär varandra vid punkt O (se figur 2).
Relationer och formler
Trapesformad höjd h
h = c
Omkrets P
Det är måttet på konturen och beräknas genom att lägga till sidorna:
Perimeter = a + b + c + d
Sidan d uttrycks i termer av höjd eller sida c med Pythagoras sats:
d = √ (a-b)två + ctvå
Byt ut i omkretsen:
P = a + b + c + √ (a-b)två + ctvå
Mellersta bas
Det är semisumman av baserna:
Medelbas = (a + b) / 2
Ibland hittas medelbasen uttryckt på detta sätt:
Medelbas = (Major bas + mindre bas) / 2
Område
Området A för trapetsformen är produkten av den genomsnittliga basen gånger höjden:
A = (Major bas + mindre bas) x höjd / 2
A = (a + b) c / 2
Diagonaler, sidor och vinklar
Flera trianglar visas i figur 2, både rätt och icke-rätt. Pythagoras sats kan tillämpas på de som är rätt trianglar och på de som inte är det, cosinus- och sinussatserna.
På detta sätt finns relationer mellan sidorna och mellan sidorna och trapezens inre vinklar..
CPA-triangel
Det är en rektangel, dess ben är lika och är värda b, medan hypotenusen är diagonalen d1, Således:
d1två = btvå + btvå = 2btvå
DAB-triangel
Det är också en rektangel, benen är till Y c (eller också till Y h) och hypotenusen är dtvå, så att:
dtvåtvå = atvå + ctvå = atvå + htvå
CDA triangel
Eftersom denna triangel inte är en rätt triangel, tillämpas cosinus-satsen på den, eller också sinus-satsen.
Enligt kosinussatsen:
d1två = atvå + dtvå - 2ad cos α
CDP-triangeln
Denna triangel är en rätt triangel och med sina sidor är de trigonometriska förhållandena för vinkeln a konstruerade:
sin α = h / d
cos a = PD / d
Men sidan PD = a - b, därför:
cos α = (a-b) / d → a - b = d cos α
a = b + d cos α
Du har också:
tg α = sin α / cos α = h / (a-b) → h = tg α (a-b)
CBD triangel
I den här triangeln har vi vinkeln vars topp är vid C. Det är inte markerat i figuren, men i början var det markerat att det är 180 - α. Denna triangel är inte en rätt triangel, så kosinosatsen eller sinussatsen kan tillämpas..
Nu kan det enkelt visas att:
sin (180 - α) = sin α
cos (180 - α) = - cos α
Tillämpa kosinussatsen:
dtvåtvå = dtvå + btvå - 2db cos (180 - a) = dtvå + btvå + 2db cos α
Exempel på rätt trapezoider
Trapezoider och i synnerhet rätt trapezoider finns på många sidor, och ibland inte alltid i konkret form. Här har vi flera exempel:
Trapesformen som designelement
Geometriska figurer finns i överflöd i arkitekturen i många byggnader, som den här kyrkan i New York, som visar en struktur i form av en rektangulär trapets..
På samma sätt är den trapesformade formen frekvent vid utformningen av behållare, behållare, blad (fräs eller exakt), märken och i grafisk design.

Trapesformad våggenerator
Elektriska signaler kan inte bara vara fyrkantiga, sinusformade eller triangulära. Det finns också trapetssignaler som är användbara i många kretsar. I figur 4 finns en trapesformad signal som består av två högra trapezider. Mellan dem bildar de en enda likbent trapez.
I numerisk beräkning
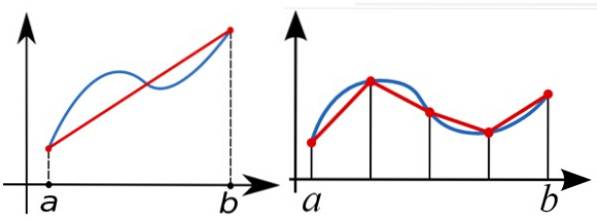
För att beräkna den bestämda integralen av funktionen f (x) mellan a och b numeriskt används trapetsregeln för att approximera arean under diagrammet för f (x). I följande figur, till vänster, integreras ungefär med en enda höger trapets.
En bättre approximation är den i rätt figur, med flera högra trapezoider.
Trapesformad laststråle
Krafter är inte alltid koncentrerade till en enda punkt, eftersom de kroppar som de agerar på har märkbara dimensioner. Så är fallet med en bro över vilken fordon cirkulerar kontinuerligt, vattnet i en pool på samma vertikala väggar eller ett tak på vilket vatten eller snö ackumuleras..
Av denna anledning fördelas krafter per längdenhet, ytarea eller volym, beroende på vilken kropp de verkar på..
I fallet med en stråle kan en kraft fördelad per längdenhet ha olika fördelningar, till exempel den högra trapetsen som visas nedan:
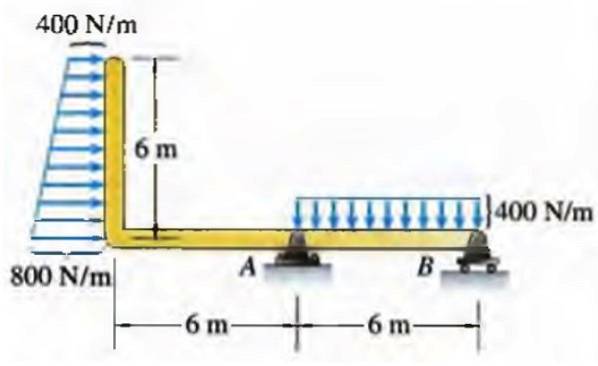
I verkligheten motsvarar inte distributioner alltid vanliga geometriska former som den här, men de kan vara en bra approximation i många fall..
Som ett pedagogiskt och lärande verktyg
Block och bilder med geometriska former, inklusive trapezoider, är mycket användbara för barn att bli bekanta med den fascinerande geometrivärlden från tidig ålder.

Lösta övningar
- Övning 1
I höger trapets i figur 1 är den större basen 50 cm och den mindre basen är lika med 30 cm, det är också känt att den sneda sidan är 35 cm. Hitta:
a) Vinkel α
b) Höjd
c) Omkrets
d) Genomsnittlig bas
e) Område
f) Diagonaler
Lösning till
Uttalandedata sammanfattas enligt följande:
a = huvudbas = 50 cm
b = mindre bas = 30 cm
d = lutande sida = 35 cm
För att hitta vinkeln α besöker vi formler och ekvationer för att se vilken som bäst passar de angivna uppgifterna. Den sökta vinkeln finns i flera av de analyserade trianglarna, till exempel CDP.
Där har vi den här formeln, som innehåller det okända och även de data som vi känner till:
cos a = (a-b) / d
Därför:
a = bågar [(a-b) / d] = bågar [(50-30) / 35] = bågar 20/35 = 55,15 º
Lösning b
Från ekvationen:
sin a = h / d
Det rensar h:
h = d. sin α = 35 sin 55,15 º cm = 28,72 cm
Lösning c
Omkretsen är summan av sidorna, och eftersom höjden är lika med sidan c har vi:
c = h = 28,72 cm
Därför:
P = (50 + 30 + 35 + 28,72) cm = 143,72 cm
Lösning d
Medelbasen är halvsumman av baserna:
Mittbotten = (50 + 30 cm) / 2 = 40 cm
Lösning e
Trapezoidens område är:
A = genomsnittlig bas x höjd = 40 cm x 28,72 = 1148,8 cmtvå.
Lösning f
För diagonal d1 du kan använda den här formeln:
d1två = btvå + btvå = 2btvå
d1två= 2 x (30 cm)två = 1800 cmtvå
d1 = √1800 cmtvå = 42,42 cm
Och för diagonalen dtvå:
dtvåtvå = dtvå + btvå + 2db cos α = (35 cm)två + (30 cm)två + 2 x 35 x 30 cmtvå cos 55,15 º = 3325 cmtvå
dtvå = √ 3325 cmtvå = 57,66 cm
Detta är inte det enda sättet att hitta dtvå, eftersom det också finns DAB-triangeln.
- Övning 2
Följande diagram över hastighet som en funktion av tiden tillhör en mobil som har enhetligt accelererad rätlinjig rörelse. Beräkna mobilens avstånd under tidsintervallet mellan 0,5 och 1,2 sekunder.
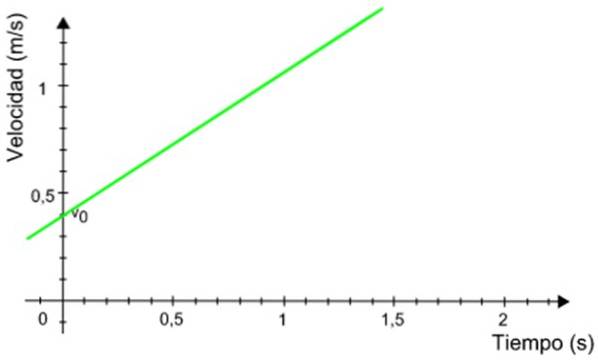
Lösning
Avståndet med mobilen är numeriskt ekvivalent med området under diagrammet, avgränsat med det angivna tidsintervallet.
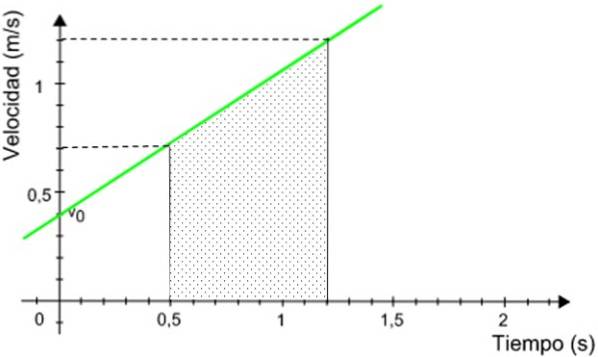
Det skuggade området är området för en höger trapets, givet av:
A = (Major bas + mindre bas) x höjd / 2
A = (1,2 + 0,7) m / s x (1,2 - 0,5) s / 2 = 0,665 m
Referenser
- Baldor, A. 2004. Plan- och rymdgeometri med trigonometri. Kulturella publikationer.
- Bedford, A. 1996. Statics. Addison Wesley Interamericana.
- Jr. geometri. 2014. Polygoner. Lulu Press, Inc..
- OnlineMSchool. Rektangulär trapets. Återställd från: es.onlinemschool.com.
- Problemlösare för automatisk geometri. Trapesen. Återställd från: scuolaelettrica.it
- Wikipedia. Trapes (geometri). Återställd från: es.wikipedia.org.



Ingen har kommenterat den här artikeln än.