De medelvinkelhastighet Rotation definieras som den vinkel som roteras per tidsenhet för positionsvektorn för en punkt som beskriver cirkelrörelse. Bladen på en takfläkt (som den som visas i figur 1) följer cirkulär rörelse och deras genomsnittliga rotationshastighet beräknas genom att ta kvoten mellan den roterade vinkeln och den tid då vinkeln färdades..
Reglerna som rotationsrörelse följer liknar något av de välbekanta för translationell rörelse. De sträckta avstånden kan också mätas i meter, men vinkelstorlekarna får särskild relevans eftersom de i hög grad underlättar beskrivningen av rörelsen.
I allmänhet används grekiska bokstäver för vinkelmängderna och latinska bokstäver för motsvarande linjära kvantiteter..
Artikelindex
Figur 2 representerar rörelsen för en punkt på en cirkulär bana c. Punktens position P motsvarar ögonblicket t och vinkelpositionen som motsvarar det ögonblicket är ϕ.
Från ögonblicket t förgår en tidsperiod Δt. Under den perioden är punktens nya position P 'och vinkelpositionen har ökat med en vinkel A.
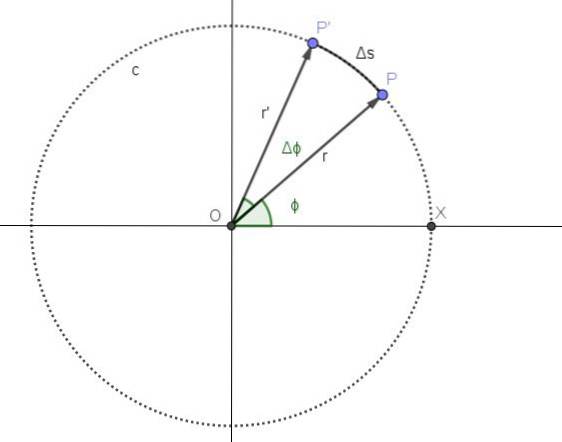
Den genomsnittliga vinkelhastigheten ω är den vinkel som har färdats per tidsenhet, så att kvoten Δϕ / Δt representerar den genomsnittliga vinkelhastigheten mellan tiderna t och t + Δt:
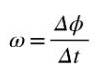
Eftersom vinkel mäts i radianer och tid i sekunder är enheten för medelvinkelhastighet rad / s. Om du vill beräkna vinkelhastighet direkt vid ögonblicket t, då måste vi beräkna kvoten Δϕ / Δt när Δt ➡0.
En rotationsrörelse är likformig om vinkeln i samma ögonblick är densamma under samma tidsperiod. Om rotationen är enhetlig sammanfaller vinkelhastigheten när som helst med medelvinkelhastigheten.
I en enhetlig rotationsrörelse kallas tiden för en fullständig revolution period och betecknas med T.
Vidare, när en hel sväng görs, är den färdade vinkeln 2π, så i en enhetlig rotation är vinkelhastigheten related relaterad till perioden T, med följande formel:
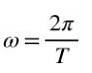
Det definierar frekvens F med en enhetlig rotation som kvoten mellan antalet varv och tiden som används för att gå igenom dem, det vill säga om N varv görs under tidsperioden At då kommer frekvensen att vara:
f = N / At
Eftersom en sväng (N = 1) färdas i tid T (perioden) erhålls följande förhållande:
f = 1 / T.
Det vill säga, i en jämn rotation är vinkelhastigheten relaterad till frekvensen genom förhållandet:
ω = 2π ・ f
Linjär hastighet v, är kvoten mellan avståndet och den tid det tar att resa. I figur 2 är det sträckta avståndet båglängden Δs.
Bågen Δs är proportionell mot den vinklade Δϕ och radien r, varvid följande förhållande uppfylls:
Δs = r ・ Δϕ
Så länge Δϕ mäts i radianer.
Om vi delar föregående uttryck med tidsförloppet Δt får vi:
(Δs / Δt) = r ・ (Δϕ / At)
Kvoten för det första elementet är linjär hastighet och kvoten för det andra elementet är medelvinkelhastigheten:
v = r ・ ω
Spetsarna på takfläktens blad som visas i figur 1 rör sig med en hastighet på 5 m / s och knivarna har en radie på 40 cm.
Beräkna med dessa data: i) hjulets genomsnittliga vinkelhastighet, ii) antalet varv hjulet gör på en sekund, iii) perioden i sekunder.
i) Linjär hastighet är v = 5 m / s.
Radien är r = 0,40 m.
Från förhållandet mellan linjär hastighet och vinkelhastighet löser vi det senare:
v = r ・ ω => ω = v / r = (5 m / s) / (0,40 m) = 12,57 rad / s
ii) ω = 2π ・ f => f = ω / 2π = (12,57 rad / s) / (2π rad) = 2 varv / s
iii) T = 1 / f = 1 / (2 varv / s) = 0,5 s för varje varv.
En leksaksvagn rör sig på ett cirkulärt spår med en radie på 2 meter. Vid 0s är dess vinkelposition 0 rad, men efter tiden t är dess vinkelposition
φ (t) = 2 ・ t .
Med dessa uppgifter
i) Beräkna medelvinkelhastigheten under följande tidsintervall [0s, 0,5s]; [0,5s, 1,0s]; [1.0s, 1.5s] och slutligen under perioden [0.0s, 1.5s].
ii) Baserat på resultaten från del i) Vad kan man säga om rörelsen?
iii) Bestäm den genomsnittliga linjära hastigheten under samma tidsperiod från del i)
iv) Hitta vinkelhastigheten och linjär hastighet för alla ögonblick.
i) Medelvinkelhastigheten ges med följande formel:
Vi fortsätter att beräkna den färdade vinkeln och tiden som gått i varje intervall.
Intervall 1: Δϕ = ϕ (0,5s) - ϕ (0,0s) = 2 (rad / s) * 0,5s - 2 (rad / s) * 0,0s = 1,0 rad
Δt = 0,5s - 0,0s = 0,5s
ω = Δϕ / Δt = 1,0rad / 0,5s = 2,0 rad / s
Intervall 2: Δϕ = ϕ (1.0s) - ϕ (0.5s) = 2 (rad / s) * 1.0s - 2 (rad / s) * 0.5s = 1.0 rad
At = 1,0s - 0,5s = 0,5s
ω = Δϕ / Δt = 1,0rad / 0,5s = 2,0 rad / s
Intervall 3: Δϕ = ϕ (1,5s) - ϕ (1,0s) = 2 (rad / s) * 1,5s - 2 (rad / s) * 1,0s = 1,0 rad
At = 1,5s - 1,0s = 0,5s
ω = Δϕ / Δt = 1,0rad / 0,5s = 2,0 rad / s
Intervall 4: Δϕ = ϕ (1,5s) - ϕ (0,0s) = 2 (rad / s) * 1,5s - 2 (rad / s) * 0,0s = 3,0 rad
Δt = 1,5s - 0,0s = 1,5s
ω = Δϕ / Δt = 3,0rad / 1,5s = 2,0 rad / s
ii) Med tanke på de tidigare resultaten, där den genomsnittliga vinkelhastigheten beräknades i olika tidsintervall, alltid med samma resultat, verkar det indikera att det är en enhetlig cirkelrörelse. Dessa resultat är dock inte avgörande..
Sättet att säkerställa slutsatsen är att beräkna medelvinkelhastigheten för ett godtyckligt intervall [t, t ']: Δϕ = ϕ (t') - ϕ (t) = 2 * t '- 2 * t = 2 * (t '-t)
Δt = t '- t
ω = Δϕ / Δt = 2 * (t'-t) / (t'-t) = 2,0 rad / s
Detta innebär att leksaksvagnen har en konstant medelvinkelhastighet på 2 rad / s under vilken tidsperiod som helst. Men du kan gå längre om du beräknar den momentana vinkelhastigheten:
Detta tolkas som att leksaksbilen alltid har konstant vinkelhastighet = 2 rad / s.
Ingen har kommenterat den här artikeln än.